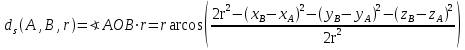Métrica
| ||||||
Métrica. En Matemáticas, Álgebra, Geometría y más específicamente, Geometría euclidiana, Geometría análitica, Topología se trata de una magnitud y su ley que determina el menor nivel de diferencia o lejanía entre dos objetos de un espacio o geometría dados, usualmente considerados puntos.
Por defecto, se refiere a la métrica euclidiana de la geometría cartesiana y sobre la cual se han elaborado el resto de los resultados de la misma. Pero en los casos en que se tienen otro tipo de geometrías, la formulación y significado de la distancia varía para adaptarse a esa situación. Por ejemplo, si bien la distancia euclideana basada en la idea de que la menor distancia entre dos puntos es la longitud del segmento de recta que los une, en el caso de la geometría esférica la menor distancia sería la longitud del arco de circunferencia máxima u ortodrómica que une los puntos. En otros espacios, pueden ser otros tipos de curvas.
Como se ve el concepto mismo de métrica se ajusta a cada situación, creando incluso casos abstractos de geometrías y espacios métricos. Aunque en cualquier caso, deben satisfacer una serie de propiedades que determinan el alcance del concepto "distancia".
Sumario
Definiciones
Se denomina métrica o distancia a toda función binaria d(x,y), donde ![]() , donde A es un conjunto no vacío cualquiera y que satisface cada una de las propiedades siguientes:
, donde A es un conjunto no vacío cualquiera y que satisface cada una de las propiedades siguientes:
- No negatividad: d(x,y)≥0.
- Simetría: d(x,y)=d(y,x).
- Reflexividad: d(x,x)=0.
- Desigualdad triangular: d(x,y)+d(y,z)≥d(x,z).
- Implicación de reflexividad: Si d(x,y)=0, entonces x=y.
Ejemplos
Existen varias formulaciones de la distancia que se aplica en distintos casos. A continuación veamos algunas de ellas.
Métrica euclideana
Artículo principal "Métrica euclideana".
Sea un espacio cartesiano de N dimensiones la distancia entre dos de sus puntos A, B viene definida por la longitud del segmento de línea recta que los une o lo que es lo mismo:
que para los casos del espacio tridimenional y el plano quedan representadas respectivamente por:
La demostración de las cinco propiedades inherentes a las métricas son evidentes.
Métrica binaria
Artículo principal "Métrica binaria".
Se define por distancia binaria a la funcion d(x,y) definida según:
Esta métrica suele ser usada en la lógica, la topología y la inteligencia artificial.
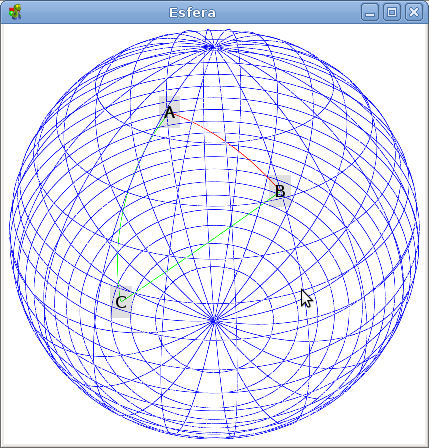
Métrica esférica
Artículo principal "Métrica esférica".
La métrica esférica es una forma de distancia que asume que los puntos A y B están dispuestos sobre la superficie de una esfera sólida centrada en O de radio "r" entonces la distancia en cuestión entre ambos puntos sería la longitud de la ortodrómica o arco de circunferencia concéntrica en O y de radio r que contiene en cada uno de sus extremos a A y a B:
Hablando númericamente sería:
donde los alfas representan las longitudes de sus respectivos puntos y las betas son las latitudes, exactamente igual que en nuestro planeta.
En el caso, por ejemplo, de las distancias marítimas, pues a nivel del mar se evade el extra en altitud que le agregan las elevaciones a los cálculos de distancia, esta forma de medición en muy útil, pues como se sabe la Tierra tiene forma esférica y sería equívoco por tanto creer que se viaja en línea recta cuando en verdad se navega sobre un arco de circunferencia.
Importancia
Las métricas son un elemento definitorio de las geometrías, espacios topológicos y otros entes matemáticos. Pero también son de vital importancia en otros terrenos toda vez que la distancia asigna a la diferencia entre objetos un valor numérico que permite cuantificar y comparar esta relación de la forma "cuán distinto es el objeto A de B".
Este rasgo es vital por ejemplo en el procesamiento de texto, donde hace falta muchas veces notar la distancia sintáctica entre vocablos para su agrupamiento en familias de palabras, como son las formas verbales de un verbo, o también en la corrección ortográfica porque cuando se detecte un error normalmente se hace contrastando la palabra con otras de un diccionario de idioma y si el rango de separación mínimo supera un valor determinado se declara como error y se proponen posibles sugerencias de sustitutos. En las formas de calcular las distancias entre palabras pueden citarse las distancias de Levenshtein, Oliver o las de pronunciación fonética, como las de Donald Knuth o la de Lawrence Philips.
Es de gran importancia en Inteligencia Artificial en las áreas de reconocimiento de patrones, minería de datos, clustering, recuperación de información, lógica no binaria, etc.
Esto se extiende a los softwares de la Química donde se revisan la diferencias estructurales entre moléculas que se traduce en diferencias de propiedades y comportamiento más o menos deseables según sea el caso.
Veáse también
- Métrica euclidiana.
- Métrica de Mahalanobis.
- Métrica esférica.
- Métrica binaria.
- Espacio métrico.
- Distancia de Levenshtein.
Fuentes
- I. Bronshtein, K. Semendiaev. Manual de matemáticas para ingenieros y estudiantes. 2da Edición. Editorial MIR, Moscú. 1973.
- Colectivo de autores. PHP Manual (PHP 5). String functions. Versión HTML del repositorio de Debian Lenny. 2008
- Distancia en Wikipedia. Revisado 29 de mayo de 2012.