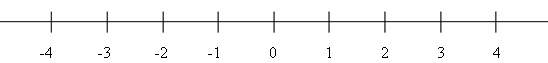Números enteros
| ||||||
Números enteros. Es el conjunto formado por los números naturales y sus opuestos.
Sumario
- 1 Definición
- 2 Tipo de enteros
- 3 Representación de los números enteros sobre una recta
- 4 Representación de los números enteros sobre el plano
- 5 Orden de los números enteros
- 6 Suma de números enteros
- 7 Suma de un entero positivo sobre la recta numérica
- 8 Suma de un entero negativo sobre la recta numérica
- 9 Resta de números enteros
- 10 Multiplicación de números enteros
- 11 Ver además
- 12 Fuentes
Definición
Un numero entero es cualquier elemento del conjunto formado por los números naturales, sus opuestos (versiones negativas de los naturales) y el cero.
Estos son:
- Los naturales (o enteros positivos): +1, +2, +3, +4, +5...
- El cero, que no es ni positivo ni negativo.
- Los enteros negativos: -1, -2, -3, -4, -5...
El conjunto de los enteros se designa por Z, (nótese que no es una Z). En notación matemática:
![]()
Tipo de enteros
- Si a, b y c son números enteros tales que a = bc, a es un múltiplo de b o de c, y b y c son divisores de a. Si c es distinto de ±1, entonces b se denomina divisor propio de a.
- Los enteros pares son los múltiplos de 2, incluyendo el 0, como -4, 0, 2 y 10;
- Un entero impar es aquél que no es par, por ejemplo, -5, 1, 3, 9.
- Un número perfecto es aquel entero positivo que es igual a la suma de todos sus divisores propios positivos (partes alícuotas); por ejemplo, 6 (que es igual a 1 + 2 + 3) y 28 (que es igual a 1 + 2 + 4 + 7 + 14) son números perfectos.
- Un entero positivo que no es perfecto se denomina imperfecto y puede ser deficiente o superante según que la suma de sus divisores propios positivos sea menor o mayor que él. Así, 9, cuyos divisores son 1 y 3, es deficiente, y 12, cuyos divisores son 1, 2, 3, 4 y 6, es superante.
Resumen
- Todos los números enteros mayores de cero se consideran positivos, y sus opuestos, se consideran negativos.
- El cero no es positivo, ni negativo, luego el opuesto del cero es el propio cero.
- El conjunto formado por el cero y todos los números enteros positivos, se denomina conjunto de los números enteros no negativos.
- El conjunto formado por el cero y todos los números enteros negativos, se denomina conjunto de los números enteros no positivos.
- Los números opuestos están situados en la recta numérica simétricamente respecto al cero.
- Los números enteros que solo se diferencian en el signo, se llaman opuestos, por ejemplo, 20 y -20 son números opuestos.
- El módulo o valor absoluto de cualquier número entero nunca es negativo. Dos números enteros opuestos tienen el mismo módulo, por ejemplo:
Representación de los números enteros sobre una recta
Se representan sobre una recta, llamada recta numérica, así:
El cero en mitad de la recta, los enteros negativos a la izquierda del cero y los enteros positivos a su derecha. Normalmente no se escribe el signo + que precede a los enteros positivos.
Representación de los números enteros sobre el plano
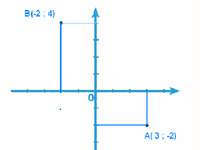
Para describir la posición de cualquier punto sobre un plano, se usa ejes de coordenadas, de forma que cada punto tendrá dos coordenadas: una sobre el eje horizontal (eje x o eje de las abscisas) y la otra sobre el vertical (eje y o eje de las ordenadas). <br
Dichas coordenadas serán números enteros.
Por ejemplo, el punto A tiene 3 unidades de coordenada horizontal y -2 de coordenada vertical. El punto B tiene -2 unidades de coordenada horizontal y 4 unidades de coordenada vertical.
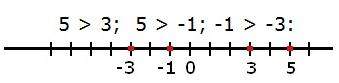
Orden de los números enteros
Un número entero es mayor que otro (lo que se indica con el símbolo >) si está situado más a la derecha sobre la recta numérica.
De la misma forma, un número entero es menor que otro (símbolo <) si está situado a la izquierda sobre la recta numérica. <br>

Suma de números enteros
Para sumar dos números enteros se procede del siguiente modo:
- Si tienen el mismo signo, se suman sus valores absolutos, y al resultado se le pone el signo que tenían los sumandos:
Ejemplo:
7 + 11 = 18
-7 - 11 = -18
- Si tienen distintos signos, es decir, si un sumando es positivo y el otro negativo, se restan sus valores absolutos y se le pone el signo del mayor:
Ejemplo:
La suma de números enteros tiene las propiedades siguientes:
- Asociativa: (a + b) + c = a + (b + c)
- Conmutativa: a + b = b + a
- Elemento neutro: el cero es el elemento neutro de la suma, a + 0 = a
- Elemento opuesto: todo número entero a, tiene un opuesto –a, a + (-a) = 0
Suma de un entero positivo sobre la recta numérica
Para sumarle a cualquier número entero otro entero positivo, nos situamos sobre el punto que representa el primer sumando y avanzamos hacia la derecha tantas unidades como nos indique el segundo sumando.
Por ejemplo, para efectuar la suma -5 + 3:
- Nos situamos en el punto de la recta que representa – 5:
2. Avanzamos desde ese punto tres unidades hacia la derecha:
3. Hemos alcanzado el punto –2. Así pues: -5 + 3 = -2.
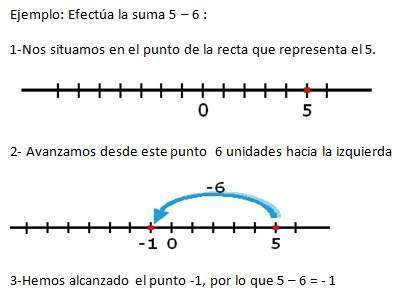
Suma de un entero negativo sobre la recta numérica
Para sumarle a cualquier número entero otro entero negativo, se sitúa sobre el punto que representa el primer sumando y se avanza hacia la izquierda tantas unidades como indique el segundo sumando.
Resta de números enteros
Para restar dos números enteros se le suma al minuendo el opuesto del sustraendo: a - b = a + (-b)
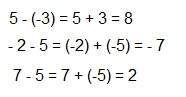
Vease también
Multiplicación de números enteros
Para multiplicar dos números enteros se multiplican sus valores absolutos y el resultado se deja con signo positivo si ambos factores son del mismo signo o se le pone el signo menos si los factores son de signos distintos. Este procedimiento para obtener el signo de un producto a partir del signo de los factores se denomina regla de los signos y se sintetiza del siguiente modo:
- + • + = +
- + • - = -
- - • + = -
- - • - = +
La multiplicación de números enteros tiene las propiedades siguientes:
- Asociativa: (a • b) • c = a • (b • c)
- Conmutativa: a • b = b • a
- Elemento neutro: el 1 es el elemento neutro de la multiplicación, a • 1 = a <br>
- Distributiva de la multiplicación respecto de la suma: a • (b + c) = a • b + a • c
Vease también
- Multiplicación y división de números negativos.
- Números Naturales
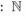
- Números racionales
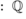
- Números complejos

Ver además
- Ábaco
- Sistema Internacional de Unidades
- Numeración decimal
- Adición y sustracción de números negativos
Fuentes
- Cuaderno complementario. Matemática 8vo grado
- Libro de texto. Matemática 7mo grado
- Rosell Franco, Sócrates. Aritmética, Volumen I, Editora Pedagógica. La Habana, 1966.