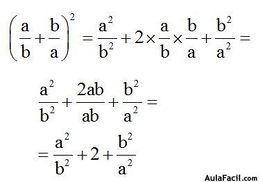Productos notables

Productos notables Concepto: Multiplicaciones cuyos productos cumplen reglas fijas.

Productos notables. Frecuentemente se presentan en álgebra multiplicaciones cuyos productos cumplen reglas fijas, a estos productos se les llama productos notables.

Cuadrado de la suma de dos términos

Elevar al cuadrado a + b equivale a multiplicar este binomio por si mismo, luego resulta: (a+b)2 = (a+b) (a+b) = a2+ab+ab+b2 = a2+2ab+b2 O sea: (a+b)2 = a2+2ab+b2 Es decir el cuadrado de una suma es igual al cuadrado del primer termino, más el duplo del primer termino por el segundo, más el cuadrado del segundo termino.

Cuadrado de la diferencia de dos términos

(a-b)2 = (a-b) (a-b) = a2-ab-ab+b2 = a2-2ab+b2 O sea: (a-b)2 = a2-2ab+b2 Se tiene entonces que el cuadrado de una diferencia es igual al cuadrado del primer termino, menos el duplo del primer termino por el segundo, más el cuadrado del segundo. Estos productos notables se diferencian solo en su signo, por lo cual podemos resumirlos de la manera siguiente (a ± b)2 = a2 ± 2ab + b2

Suma por la diferencia de dos términos

(a+b) (a-b) = a2-ab+ab-b2 = a2-b2 Luego (a+b) (a-b) = a2-b2 Por lo tanto el producto de la suma por la diferencia de dos términos, es igual a la diferencia de sus cuadrados. Producto de dos binomios que tienen un término común. (x + a ) (x + b ) = x2+bx+ax+ab = x2+(a+b) x +ab bx+ax = (a+b)x Luego (x + a) (x + b) = x2+(a+b) x +ab Por tanto el producto de dos binomios que tienen un termino común es igual al cuadrado del termino común, más la suma algebraica de los términos no comunes por el termino común, más el producto de los términos no comunes.

Descomposición factorial. Extracción del factor común

Si dos expresiones algebraicas A y B se multiplican y su producto es C, cada una de las expresiones A y B se dice que es un factor o divisor de C. Ejemplo, puesto que a( a+b) = a2+ab, se dice que a y a+b son factores o divisores de a2 + ab. Del mismo modo (x + 2) (x -2) = x2 -4, luego x+2 y x-2 son factores o divisores de x2 -4. A menudo resulta conveniente determinar los factores de una expresión algebraica dada C. La operación que consiste en hallar estos factores (cuando existen) se denomina factorización o descomposición en factores de la expresión C.

Factor común

Para descomponer en factores la expresión ma +mb, resulta aplicando la propiedad distributiva: ma + mb = m(a+b) donde m es el factor común de la expresión ma + mb, ya que dicho factor aparece en cada uno de los términos de la expresión dada. En general si en una expresión algebraica dada existe un factor que sea común a todos sus términos, esta puede descomponerse en el producto de dicho factor común por el polinomio que resulta al dividir cada uno de los términos de la expresión dada `por ese factor común.

Descomposición factorial de binomios

La suma de dos términos multiplicada por su diferencia es igual a la diferencia de sus cuadrados: (a+b) (a-b) = a2-b2 Utilizando este producto notable, se puede obtener un procedimiento para descomponer en factores una diferencia de dos cuadrados La diferencia de dos cuadrados se descompone en el producto de la suma por la diferencia de las bases de sus cuadrados En símbolos: a2-b2 = (a+b) (a-b)

Descomposición factorial de trinomios

Trinomio cuadrado perfecto. Todo trinomio que sea cuadrado perfecto se puede transformar en el cuadrado de un binomio. Un trinomio es cuadrado perfecto si: • Dos de sus términos son cuadrados perfectos, y • el término restante es igual al doble producto de las raíces cuadradas de dichos términos, o al opuesto de dicho producto.

El trinomio se descompone en el cuadrado de la suma o de la diferencia de las raíces cuadradas de los términos cuadrados perfectos, según el signo del término restante sea positivo o negativo. a2 ± 2ab + b2 = (a ± b)2

Trinomio de la forma x2+ px + q

Un trinomio de la forma x2+ px + q se puede descomponer en el producto de dos factores (x+a) y (x+b) siempre que podamos encontrar dos números a y b cuya suma algebraica sea p y cuyo producto sea q, y se tiene entonces: x2+ px + q = (x+a) (x+b), donde a+b=p y ab = q.

Trinomio de la forma mx2+ px + q, m ≠ 1

De modo general se cumple (ax +b)(cx + d) = acx2+(ad + bc)x + bd = m x2+ px +q Donde m = ac, q = bd y p = ad + bc. Por lo tanto, siempre que sea posible determinar los números a, b, c y d, tales que: ac = m, bd = q y ad = bc = p se cumple m x2+ px +q = (ax +b) (cx + d) Los trinomios de la forma mx2+ px + q, (m ≠ 1) también pueden descomponerse en factores reduciéndolos a la forma x2+ px +q. para ello se utiliza el procedimiento siguiente: Se multiplica y se divide el trinomio dado por m, con lo que se obtiene: m x2+ px +q = (mx)2 + p(mx) + mq m Así, el numerador queda reducido a la forma x2+ px +q y considerando mx como una sola variable, se procede a descomponer dicho numerador en un producto de la forma (mx +a)(mx +b) siempre que sea posible encontrar dos números que multiplicados den mq y que sumados den p.

Fuentes

• Libro de texto 9no grago Matemática.