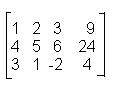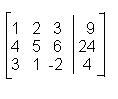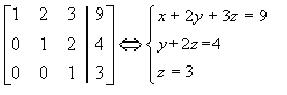Sistemas lineales de tres ecuaciones
| ||||||
Sistemas lineales de tres ecuaciones. Son sistemas que pueden tener solución única, un número infinito de soluciones o no tener solución.
Sumario
Historia
Los sistemas de ecuaciones lineales fueron ya resueltos por los babilonios, los cuales llamaban a las incógnitas con palabras tales como longitud, anchura, área, o volumen, sin que tuvieran relación con problemas de medida.
Un ejemplo tomado de una tablilla babilónica plantea la resolución de un sistema de ecuaciones en los siguientes términos:
1/4 anchura + longitud = 7 manos
longitud + anchura = 10 manos
Para resolverlo comienzan asignando el valor 5 a una mano y observaban que la solución podía ser: anchura = 20, longitud = 30. Para comprobarlo utilizaban un método parecido al de eliminación. En notación, sería:
y + 4x = 28
y + x = 10
Restando la segunda de la primera, se obtiene 3x = 18 , es decir: x = 6 e y = 4 .
También resolvían sistemas de ecuaciones, donde alguna de ellas era cuadrática. Los griegos también resolvían algunos sistemas de ecuaciones, pero uti1izando métodos geométricos. Thymaridas (400 a. de C.) había encontrado una fórmula para resolver un determinado sistema de n ecuaciones con n incógnitas.
Diophante resuelve también problemas en los que aparecían sistemas de ecuaciones, pero transformándolos en una ecuación lineal. Diophante sólo aceptaba las soluciones positivas, pues lo que buscaba era resolver problemas y no ecuaciones. Utilizó ya un álgebra sincopada como hemos señalado anteriormente. Sin embargo, unas de las dificultades que encontramos en la resolución de ecuaciones por Diophante es que carece de un método general y utiliza en cada problema métodos a veces excesivamente ingeniosos. Los sistemas de ecuaciones aparecen también en los documentos indios. No obstante, no llegan a obtener métodos generales de resolución, sino que resuelven tipos especiales de ecuaciones.
El libro "El arte matemático" , de autor chino desconocido (siglo III a. de C.), contiene algunos problemas donde se resuelven ecuaciones. En ellos encontramos un esbozo del método de las matrices para resolver sistemas de ecuaciones lineales. Uno de dichos problemas equivale a resolver un sistema de tres ecuaciones lineales por dicho método matricial.
Solución de los sistemas de tres ecuaciones con tres variables
En un sistema de tres ecuaciones con tres incógnitas. Cada una de las ecuaciones representa un plano. De acuerdo con las posibles relaciones que se den entre los tres planos, se determina el tipo de solución que tiene el sistema:
Sistemas de tres ecuaciones con tres incógnitas que no tienen solución:
- Tres planos paralelos.
- Dos planos paralelos y otro los corta.
- Plano paralelo a la línea de corte de los otros dos.
- Dos planos superpuestos y el otro paralelo.
Sistemas de tres ecuaciones con tres incógnitas que tienen infinitas soluciones
- Tres planos superpuestos.
- Haz de planos.
- Dos planos superpuestos y otro que los corta.
Sistemas de tres ecuaciones con tres incógnitas que tienen solución única
- Tres planos que se cortan en un punto.
Método de eliminación para resolver un sistema de ecuaciones
A continuación, a través de un ejemplo se mostrará como dar solución a un sistema lineal de tres ecuaciones.
Ejemplo:
Resuelve el sistema:
x + 2y + 3z = 9 ............................ (primer ecuación)
4x + 5y + 6z = 24 .......................... (segunda ecuación)
3x + y - 2z = 4 ............................ (tercera ecuación)
Solución:
Suma (-4) veces la "primera ecuación" a la "segunda":
x + 2y + 3z = 9
-3y - 6z = -12
3x + y - 2z = 4
Suma (-3) veces la "primera ecuación" a la "tercera":
x + 2y + 3z = 9
-3y - 6z = -12
-5y - 11z = -23
Multiplica por -(1/3) la "segunda ecuación":
x + 2y + 3z = 9
y + 2z = 4
-5y -11z = -23
Multiplica por (-1) la "tercera ecuación":
x + 2y + 3z = 9
y + 2z = 4
5y +11z = 23
Suma (-5) a la "segunda ecuación" y "tercera ecuación":
x + 2y + 3z = 9
y + 2z = 4
z = 3
Las soluciones del último sistema son fáciles de hallar por sustitución.
De la "tercera ecuación", vemos que z = 3.
Al sustituir "z" con 3 en la "segunda ecuación", y + 2z = 4 se obtiene y =(-2)
Por último, encontramos el valor de "x" al sustituir y =(-2) y z = 3, en la "primera ecuación", x + 2y + 3z = 9 con lo cual x = 4.
Por tanto, hay una solución:
x = 4
y =(-2)
z = 3
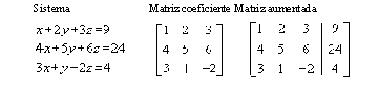
Método de las matrices para resolver sistemas de ecuaciones de tres variables
Analizando el método utilizado en el ejemplo anterior para dar solución a un sistema de ecuaciones de tres incognitas, pudimos percatarnos que los símbolos usados para las variables carecen de importancia, y solo se tuvo en cuenta los coeficientes de las mismas. Pero es posible simplificar el proceso si se introduce un esquema con los coeficientes, de forma tal, que no haya necesidad de escribir las variables.
Primero se comprobó que las variables aparecieran en el mismo orden en cada ecuación y que los términos sin variables estuviesen a la derecha de los signos de igualdad. Para ello utilizaremos el mismo ejemplo del epígrafe anterior, quedando de la siguiente manera:
Una ordenación de números de este tipo se llama matriz.
Los renglones (o filas) de la matriz son los números que aparecen uno a continuación del otro en sentido horizontal:
| 1 | 2 | 3 | 9 | Primer renglón(R1) |
|---|---|---|---|---|
| 4 | 5 | 6 | 24 | segundo renglón(R2) |
| 3 | 1 | -2 | 4 | tercer renglón(R3) |
Las columnas de la matriz son los números que aparecen uno junto del otro en sentido vertical.
| Primera columna C1 | Segunda columna C2 | Tercera columna C3 | Cuarta columna C4 |
|---|---|---|---|
| 1 | 2 | 3 | 9 |
| 4 | 5 | 6 | 24 |
| 3 | 1 | -2 | 4 |
La matriz obtenida del sistema de ecuaciones lineales del modo anterior es la matriz del sistema. Si borramos la última columna, la restante ordenación es la matriz de coeficiente. En vista de que podemos tener la matriz del sistema a partir de la matriz coeficiente agregando una columna, le decimos matriz coeficiente aumentada o simplemente matriz aumentada. Después, cuando se utilicen matrices para hallar las soluciones de un sistema de ecuaciones lineales, se introducirá un segmento de línea vertical en la matriz aumentada, a fin de indicar dónde aparecerían los signos de igualdad en el sistema de ecuaciones correspondiente.
Para resolver el sistema:
x + 2y + 3z = 9
4x + 5y + 6z = 24
3x + y - 2z = 4
Comenzaremos con la matriz del sistema, es decir, la matriz aumentada
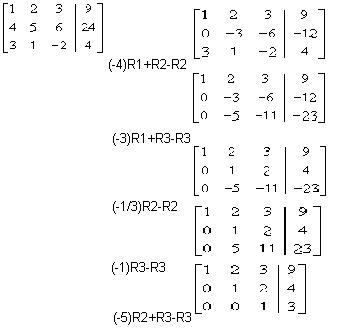
Luego aplicamos transformaciones elementales de renglón a fin de obtener otra matriz (más sencilla) de un sistema de ecuaciones equivalentes. Pondremos símbolos adecuados entre matrices equivalentes.
Con la matriz final regresamos al sistema de ecuaciones:
Que equivale al sistema original. La solución x = 4, y = -2, z = 3 se puede encontrar ahora por sustitución.
La matriz final de la solución es una forma escalonada.
Fuentes
- Artículo Sistema de ecuaciones. lineales. Disponible en la Web "wikipedia.org". Consultado el 28 de junio del 2011.
- Artículo Sistemas de tres. Disponible en ¨www.ematematicas.net¨. Consultado el 28 de junio del 2011.
- Artículo Ecuaciones. Disponible en ¨www.vitutor.com¨. Consultado el 28 de junio del 2011.
