Tablas de la verdad
| ||||||
Tablas de verdad o tabla de valores de verdad, es una tabla que muestra el valor de verdad de una proposición compuesta, para cada combinación de valores de verdad que se pueda asignar a sus componentes.
Sumario
Origen
Fue desarrollada por Charles Sanders Peirce por los años 1880, pero el formato más popular es el que introdujo Ludwig Wittgenstein en su Tractatus logico-philosophicus, publicado en 1921.| P | Ø P |
| 1 | 0 |
| 0 | 1 |
Qué son las tablas de la verdad
Las tablas de verdad son, por una parte, uno de los métodos más sencillos y conocidos de la lógica formal, pero la mismo tiempo también uno de los más poderosos y claros. Entender bien las tablas de verdad es, en gran medida, entender bien a la lógica formal misma.
| P | Q | ^Q |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
- . Sin son tautológicas, contradictorias o contingentes
- . Cuáles son sus condiciones de verdad
- . Cuál es su rol inferencial, es decir, cuáles son sus conclusiones lógicas y de qué otras proposiciones se siguen lógicamente.
Las tablas de la verdad
Estas tablas pueden construirse haciendo una interpretación de los signos lógicos como: no, o, y, si…entonces, sí y sólo si. La interpretación corresponde al sentido que estas operaciones tienen dentro del razonamiento. Puede establecerse una correspondencia entre los resultados de estas tablas y la deducción lógico matemática. En consecuencia, las tablas de verdad constituyen un método de decisión para chequear si una proposición es o no un teorema. Para la construcción de la tabla se asignará el valor 1(uno) a una proposición cierta y 0 (cero) a una proposición falsa.
- Negación: El valor de verdad de la negación es el contrario de la proposición negada.
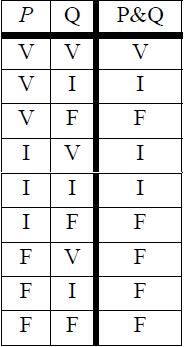
- La conjunción sirve para indicar que se cumplen dos condiciones simultáneamente, por ejemplo:
La función es creciente y está definida para los números positivos, utilizamos Para que la conjunción p^q sea verdadera las dos expresiones que intervienen deben ser verdaderas y sólo en ese caso como se indica por su tabla de verdad.
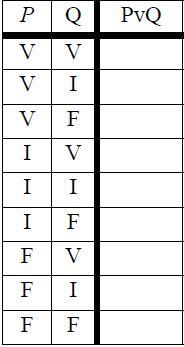
- Disyunción: La disyunción solamente es falsa si lo son sus dos componentes.
Con la disyunción a diferencia de la conjunción, se representan dos expresiones que afirman que una de las dos es verdadera, por lo que basta con que una de ellas sea verdadera para que la expresión p ∨ q sea verdadera.
- Condicional: El condicional solamente es falso cuando el antecedente es verdadero y el consecuente es falso. De la verdad no se puede seguir la falsedad.
| P | Q | PVQ |
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
| 0 | 0 | 0 |
- Bicondicional:El bicondicional solamente es cierto si sus componentes tienen el mismo valor de verdad.
| P | Q | P®Q |
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
| 0 | 0 | 1 |
Se denomina tautología una proposición que es cierta para cualquier valor de verdad de sus componentes. Por tanto, la última columna de su tabla de verdad estará formada únicamente por unos. Contradicción es la negación de una tautología, luego es una proposición falsa cualesquiera sea el valor de verdad de sus componentes. La última columna de la tabla de verdad de una contradicción estará formada únicamente por ceros.
Tablas de verdad trivalentes
Las tablas de verdad tradicionales pueden rescribirse si se dejan vacías casillas en las que el valor de verdad de la fórmula atómica es irrelevante, por ejemplo, la tabla de la disyunción:
Las primeras dos líneas señalan que no importa cuál sea el valor de verdad de uno de los disyuntos, siempre que el otro sea verdadero, la disyunción será verdadera. De la misma manera, se podría abreviar la tabla de la conjunción de la siguiente manera:
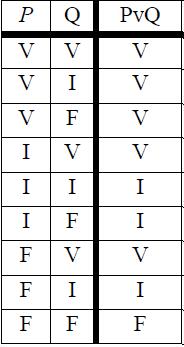
Las últimas dos líneas señalan que no importa cuál sea el valor de verdad de uno de los disyuntos, siempre que el otro sea falso, la conjunción será falsa. La ventaja de este tipo de tablas es que permiten extenderse de manera muy natural para permitir un tercer valor de verdad que no sea ni verdadera ni falso. Será llamado “I” por “indeterminado”. Ahora se puede usar la tabla abreviada de la disyunción clásica para desarrollar una tabla de verdad (no abreviada) para la disyunción trivalente. Primer paso: identificar las diferentes nueve posibilidades de combinaciones para dos variables
Segundo paso: Usar las primeras dos líneas de la tabla abreviada para determinar el valor de verdad de los renglones con por lo menos un argumento verdadero:
Tercer paso: Cómo la última línea de la tabla abreviada es también la última línea de la nueva tabla, le corresponde el mismo valor de verdad: falso.
Cuarto paso: Finalmente, cómo ya están los renglones que son verdaderos o falsos según la tabla original, los renglones que aún no tienen valor de verdad, dado que no son ni verdaderos (sino hubieran quedado como tales en el segundo paso) ni falsos (ya que tampoco quedaron así en el tercer paso), deben ser indeterminados!
En algunos casos, esta tabla de verdad aparece, no en tres columnas, sino en un cuadro. Lo cual tiene la ventaja de dejar más claro el patrón que emerge de la tabla. Siguiendo los mismos pasos se obtiene la tabla de la conjunción:
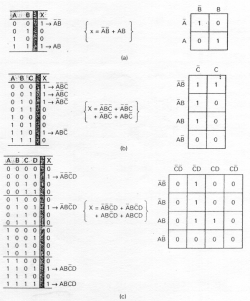
Construcción de Tablas de Verdad
Algoritmo para construir una tabla de verdad de una fórmula en lógica de proposiciones.
- Escribir la fórmula con un número arriba de cada operador que indique su jerarquía. Se escriben los enteros positivos en orden, donde el número 1 corresponde al operador de mayor jerarquía. Cuando dos operadores tengan la misma jerarquía, se le asigna el número menor al de la izquierda.
- Construir el árbol sintáctico empezando con la fórmula en la raíz y utilizando en cada caso el operador de menor jerarquía. O sea, del número mayor al menor.
- Numerar las ramas del árbol en forma secuencial empezando por las hojas hacia la raíz, con la única condición de que una rama se puede numerar hasta que estén numerados los hijos. Para empezar con la numeración de las hojas es buena idea hacerlo en orden alfabético, así todos obtienen los renglones de la tabla en el mismo orden para poder comparar resultados.
- Escribir los encabezados de la tabla las fórmulas siguiendo la numeración que se le dió a las ramas en el árbol sintáctico.
- Asignarle a los átomos, las hojas del árbol, todos los posibles valores de verdad de acuerdo al orden establecido. Por supuesto que el orden es arbitrario, pero como el número de permutaciones es n!, conviene establecer un orden para poder comparar resultados fácilmente.
- Asignar valor de verdad a cada una de las columnas restantes de acuerdo al operador indicado en el árbol sintáctico utilizando la tabla de verdad. Conviene aprenderse de memoria las tablas de los operadores, al principio pueden tener un resumen con todas las tablas mientras se memorizan.
- La última columna, correspondiente a la fórmula original, es la que indica los valores de verdad posibles de la fórmula para cada caso.
Otras tablas de verdad divergentes
Además de las tablas polivalentes e intencionales, hay muchas otras tablas de verdad. Por ejemplo, hay tablas de verdad en las que los renglones se bifurcan en dos o más sub-renglones y son útiles para lo que en lógica llamamos super-valuaciones. También existen tablas con valores y más de 2n renglones, ¿cómo es posible? Pues porque, a diferencia de las tablas tradicionales, en estas tablas el orden de los renglones sí importa, de tal manera que renglones repetidos cuentan como renglones distintos. Finalmente, también existen las tablas bidimensionales, usadas originalmente en ciertas lógicas intencionales, pero popularizadas gracias al trabajo de Robert Stalnaker y otros.
Fuentes
- Mi tecnológico. Consultado el 17 de mayo del 2012.
- Una mirada a las tablas de la verdad. Consultado el 17 de mayo del 2012.
- Tablas de la verdad. Consultado el 17 de mayo del 2012.
- Lógica proposicional. Consultado el 17 de mayo del 2012.
| P | Q | P<<Q |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
| 0 | 0 | 1 |