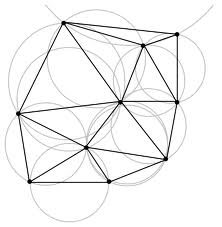
Triangulación de Delaunay
| ||||||
La triangulación de Delaunay, a veces escrito fonéticamente «triangulación de Deloné», es una red de triángulos que cumple la «condición de Delaunay». Esta condición dice que la circunferencia circunscrita de cada triángulo de la red no debe contener ningún vértice de otro triángulo. Se usan triangulaciones de Delaunay en geometría por computadora, especialmente en gráficos 3D por computadora.
Se le denomina así por el matemático ruso Borís Deloné, quien lo inventó en 1934; el mismo Deloné usó la forma francesa de su apellido, «Delaunay», como apreciación a sus antecesores franceses.
Sumario
Aplicación
En gráficos 3D por computadora se usan redes de polígonos para modelar objetos tridimensionales, juntando los polígonos para imitar la superficie del objeto. En general se usan triángulos porque son los polígonos más simples y tienen muchas propiedades favorables, como que representan una superficie coplanar.
Hay dos formas de modelar un objeto de superficies: modelarlo de mano o escanearlo con un range scanner. Al escanearlo se produce un relieve de la superficie formado por puntos discretos (ver Fig. 1). Para usar ese relieve hay que transformarlo en una red de triángulos (ver Fig. 2); esa transformación se llama «triangulación».
La triangulación de Delaunay maximiza los ángulos interiores de los triángulos de la triangulación. Eso es muy práctico porque al usar la triangulación como modelo tridimensional los errores de redondeo son mínimos. Por eso, en general se usan triangulaciones de Delaunay en aplicaciones gráficas.
Propiedades
Triangulaciones de Delaunay tienen las propiedades siguientes:
- La triangulación forma la envolvente convexa del conjunto de puntos.
- El ángulo mínimo dentro de todos los triángulos está maximizado.
- La triangulación es unívoca si en ningún borde de circunferencia circunscrita hay más que tres vértices.
Construcción del algoritmo
Hay varios algoritmos que sirven para crear una triangulación de Delaunay a partir de un conjunto de puntos. En todos estos algoritmos hay que inspeccionar si un vértice está dentro de una circunferencia circunscrita o no, así que este test tiene que ser muy eficiente. Por supuesto es posible computar el circuncentro y la circunferencia circunscrita y después examinar si el vértice está dentro del círculo, pero hay un test más simple y eficiente que usa el determinante de una matriz. En dos dimensiones. Si los tres puntos A, B y C forman un triángulo con los puntos denominados en sentido contrario al de las agujas del reloj, el punto D está dentro de su circunferencia circunscrita si:
Es decir, si el determinante de este matriz es mayor que 0. En este caso es suficiente conocer el signo aritmético, así que este cómputo puede ser acelerado fácilmente.
Construcción Incremental
- Este algoritmo añadie un vértice a una triangulación de Delaunay y corrige la red hasta que todos los triángulos cumplan de nuevo la condición de Delaunay.
Divide y Vencerás
- Este algoritmo usa el principio conocido como divide and conquer: divide el conjunto de puntos en dos partes de igual tamaño, calcula la triangulación de Delaunay para cada parte individualmente y después reune las dos triangulaciones corrigiendo los errores.
Sweepline
- El algoritmo sweepline (en español recorrer la línea) se basa en un principio similar a la construcción incremental: construir una pequeña parte de la triangulación final y después seguir añadiendo vértices hasta que la triangulación esté completa. La diferencia estriba en que no hay que corregir ningún de los errores que pudieran presentarse.
Fuentes
Triangulaciones de Delaunay
Geometría Computacional
Triangulaciones de Delaunay aplicada a modelos 2D
Triangulaciones de Delaunay (construcción incremental)