Diferencia entre revisiones de «Nomograma»
| Línea 1: | Línea 1: | ||
| − | |||
{{Definición | {{Definición | ||
|nombre=Nomograma | |nombre=Nomograma | ||
| Línea 7: | Línea 6: | ||
}} | }} | ||
| − | '''Nomograma''' | + | '''Nomograma'''. [[ábaco]] o [[nomografo]] .Es un instrumento gráfico de cálculo, un diagrama bidimensional que permite el cómputo gráfico y aproximado de una función de cualquier número de variables. En su concepción más general, el nomograma representa simultáneamente el conjunto de las ecuaciones que definen determinado problema y el rango total de sus soluciones. |
| − | |||
| − | + | ==Definición== | |
| + | Es un modelo que utiliza un algorritmo o una fórmula matemática para predecir la probabilidad de un resultado, optimizado para una mayor seguridad predictiva. | ||
| + | Los nomogramas son una herramienta de uso cotidiano.Una de sus ventajas es su utilidad para realizar la síntesis de cuadros complejos en el momento de satisfacer todas las inquietudes de los pacientes. | ||
| − | + | Por ejemplo en la práctica diaria se asiste a pacientes que exigen un mayor caudal de información sobre la enfermedad que motiva su consulta.Muchas veces demuestran que han leído suficientemente sobre el tema, exponen sus dudas respecto del pronóstico y exigen certezas sobre el tratamiento que el profesional sugiere. | |
| − | + | Esto obliga a todos los médicos a estar permanentemente actualizados, ya sea por medio de revistas, libros de textos, cursos, congresos o a través de la enorme cantidad de información médica que se encuentra en Internet.Y toda esta información debe ser resumida para que sea entendible. Esto puede hacerse con nomogramas. | |
| − | + | Ademas se trata de un instrumento de cálculo analógico, como lo es la regla de cálculo, por utilizar segmentos continuos de líneas para representar los valores numéricos discretos que pueden asumir las variables. Los nomogramas solían utilizarse en casos en que la obtención de una respuesta exacta era imposible o muy inconveniente, mientras que la obtención de una solución aproximada era suficiente y muy deseable. | |
| − | + | ==Las tablas== | |
| + | Los nomogramas están íntimamente relacionados con otro instrumento tradicional de solución de problemas y de presentación sucinta de información científica, las tablas. | ||
| + | Como decía en [[1911]] el ingeniero militar español [[Ricardo Seco]], "si fuese posible reunir en un pequeño volumen una colección de tablas donde se hallasen consignados los resultados que dan las fórmulas de más frecuente aplicación para todos los valores que en la práctica pueden tomar las distintas variables que contienen, se habría llegado al desideratum que debe tratar de llenar todo manual de carácter práctico." | ||
| − | + | Pero, añadía, "tal colección de tablas es irrealizable porque, descontado el excesivo trabajo, largo tiempo necesario para su construcción y gran volumen que ocuparían," si existiesen más de tres variables en la fórmula "no hay medio práctico de construirlas". En cambio, como ha quedado dicho, las técnicas nomográficas permiten construir nomogramas de prácticamente cualquier número de variables. | |
| − | |||
| − | |||
| − | |||
| − | |||
D'Ocagne afirmaba en Le calcul simplifié que "los nomogramas pueden considerarse como tablas de cálculos completos", añadiendo a las ventajas ya mencionadas que tienen sobre ellas la facilidad de interpolación visual, al tiempo que reconocía el inconveniente de que la precisión que pueden alcanzar los datos de las tablas es en principio tan grande como se quiera, mientras que la de los nomogramas es esencialmente muy limitada. | D'Ocagne afirmaba en Le calcul simplifié que "los nomogramas pueden considerarse como tablas de cálculos completos", añadiendo a las ventajas ya mencionadas que tienen sobre ellas la facilidad de interpolación visual, al tiempo que reconocía el inconveniente de que la precisión que pueden alcanzar los datos de las tablas es en principio tan grande como se quiera, mientras que la de los nomogramas es esencialmente muy limitada. | ||
==Su Uso== | ==Su Uso== | ||
Al ser un nomograma la representación gráfica de una ecuación de varias variables, ha de constar de tantos elementos gráficos como variables tenga la ecuación. Estos elementos serán puntos o líneas, rectas o curvas, según los casos. Dados los valores de todas las variables menos una, el de esta última puede encontrarse por medio de algún recurso geométrico inmediato (que generalmente es el trazado de otra línea que pasa por ese punto). | Al ser un nomograma la representación gráfica de una ecuación de varias variables, ha de constar de tantos elementos gráficos como variables tenga la ecuación. Estos elementos serán puntos o líneas, rectas o curvas, según los casos. Dados los valores de todas las variables menos una, el de esta última puede encontrarse por medio de algún recurso geométrico inmediato (que generalmente es el trazado de otra línea que pasa por ese punto). | ||
| + | |||
Por tanto, el nomograma de una ecuación de dos variables (y = f(x)) tendrá dos elementos gráficos, normalmente dos rectas graduadas, o escalas, dispuestas de tal modo que la determinación del valor de una de las variables (fijación de un punto de la línea) especifique el valor de la otra, la desconocida o función. El nomograma de una ecuación de tres variables (z = f(x, y)) constará normalmente de tres escalas y así sucesivamente. | Por tanto, el nomograma de una ecuación de dos variables (y = f(x)) tendrá dos elementos gráficos, normalmente dos rectas graduadas, o escalas, dispuestas de tal modo que la determinación del valor de una de las variables (fijación de un punto de la línea) especifique el valor de la otra, la desconocida o función. El nomograma de una ecuación de tres variables (z = f(x, y)) constará normalmente de tres escalas y así sucesivamente. | ||
| + | |||
El arte de la nomografía consiste precisamente en elaborar dichas escalas y disponerlas en el plano de tal manera que el trazado de líneas rectas que las atraviesen determine los puntos colineares existentes en cada una de las escalas, puntos que representarán los distintos valores relacionados por la función en cada caso concreto. | El arte de la nomografía consiste precisamente en elaborar dichas escalas y disponerlas en el plano de tal manera que el trazado de líneas rectas que las atraviesen determine los puntos colineares existentes en cada una de las escalas, puntos que representarán los distintos valores relacionados por la función en cada caso concreto. | ||
| − | La disposición relativa entre estos elementos, en cambio, no puede predecirse, pues vendrá determinada por la naturaleza del problema en cuestión o por otro tipo de consideraciones. Por ejemplo, el nomograma de la función de dos variables que relaciona los grados Celsius de temperatura con los [[Farenheit]] puede consistir en dos escalas paralelas adecuadamente situadas. Para utilizarlo bastará con colocar una regla perpendicular a la escala que contenga el dato conocido; el otro se encontrará en el punto en que la regla corte a su escala correspondiente. Pero es evidente que el espacio que separa ambas escalas no desempeña ninguna función especial, por lo que se le puede reducir progresivamente hasta el extremo de hacerlo desaparecer y que ambas se confundan en una sola, que quedará así rotulada a ambos lados, siendo entonces inmediata la lectura del resultado de la conversión. | + | |
| + | La disposición relativa entre estos elementos, en cambio, no puede predecirse, pues vendrá determinada por la naturaleza del problema en cuestión o por otro tipo de consideraciones. Por ejemplo, el nomograma de la función de dos variables que relaciona los grados Celsius de temperatura con los [[Farenheit]] puede consistir en dos escalas paralelas adecuadamente situadas. Para utilizarlo bastará con colocar una regla perpendicular a la escala que contenga el dato conocido; el otro se encontrará en el punto en que la regla corte a su escala correspondiente. | ||
| + | |||
| + | Pero es evidente que el espacio que separa ambas escalas no desempeña ninguna función especial, por lo que se le puede reducir progresivamente hasta el extremo de hacerlo desaparecer y que ambas se confundan en una sola, que quedará así rotulada a ambos lados, siendo entonces inmediata la lectura del resultado de la conversión. | ||
==Ejemplos de nomograma== | ==Ejemplos de nomograma== | ||
| Línea 40: | Línea 43: | ||
'''Un gráfico útil''' | '''Un gráfico útil''' | ||
| + | Para reducir el volumen del aire medido en ATPS se utilizará la expresión | ||
| + | Volumen aire STPD - (Volumen aire ATPS),(Factor STPD). | ||
| + | Nota: Los valores del factor STPD empiezan en 0.570 y así en orden progresivo hasta 1.020 (ejemplo: 0.750) | ||
| + | [[Archivo:Grafico-nomo3.png|100px|thumb|left|Nomograma para calcular la superficie cutánea]] | ||
| + | [[Archivo:Grafico-nomo4.png|150px|thumb|center|Nomograma para determinar el factor STPD]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | ==Historia== | ||
Los [[astrolabios]], [[cuadrantes]] y sectores de finales de la [[Edad Media]] y del [[Renacimiento]] (colectivamente llamados instrumentos matemáticos) ya estaban destinados a resolver problemas prácticos de índole matemática de forma gráfica y mecánica. | Los [[astrolabios]], [[cuadrantes]] y sectores de finales de la [[Edad Media]] y del [[Renacimiento]] (colectivamente llamados instrumentos matemáticos) ya estaban destinados a resolver problemas prácticos de índole matemática de forma gráfica y mecánica. | ||
La invención de la [[escala de Gunter]] en el [[siglo XVII]] constituyó la primera representación gráfica de una función mediante una escala graduada y fue esencial para todos los avances posteriores. Otro paso decisivo fue la invención por [[Descartes]] de la [[geometría analítica]], que permite la representación gráfica de cualquier función matemática por medio de una curva. | La invención de la [[escala de Gunter]] en el [[siglo XVII]] constituyó la primera representación gráfica de una función mediante una escala graduada y fue esencial para todos los avances posteriores. Otro paso decisivo fue la invención por [[Descartes]] de la [[geometría analítica]], que permite la representación gráfica de cualquier función matemática por medio de una curva. | ||
| + | |||
Fueron especialmente los ingenieros militares y otros funcionarios públicos, encargados de resolver regularmente problemas cuantitativos de carácter repetitivo, quienes mostraron naturalmente mayor interés en procurarse ayudas para su tarea. Así [[L. Pouchet]] publicó en [[1797]] una obra titulada Métrologie terrestre, que contiene un apéndice designado Arithmétique linéaire en el que se contiene el primer intento sistemático de construcción de tablas gráficas de doble entrada. | Fueron especialmente los ingenieros militares y otros funcionarios públicos, encargados de resolver regularmente problemas cuantitativos de carácter repetitivo, quienes mostraron naturalmente mayor interés en procurarse ayudas para su tarea. Así [[L. Pouchet]] publicó en [[1797]] una obra titulada Métrologie terrestre, que contiene un apéndice designado Arithmétique linéaire en el que se contiene el primer intento sistemático de construcción de tablas gráficas de doble entrada. | ||
| + | |||
En [[1842]] [[Léon Lalanne]] propuso el empleo de dispositivos de este género para el cálculo de desmontes y terraplenes y en [[1843]] formuló el principio de [[anamorfosis]], que facilitó mucho la construcción de estos gráficos de doble entrada, a los que llamó [[ábacos]], al sustituir en la mayoría de los casos las líneas curvas por rectas. [[J. Massau]] generalizó este principio hacia [[1880]]. | En [[1842]] [[Léon Lalanne]] propuso el empleo de dispositivos de este género para el cálculo de desmontes y terraplenes y en [[1843]] formuló el principio de [[anamorfosis]], que facilitó mucho la construcción de estos gráficos de doble entrada, a los que llamó [[ábacos]], al sustituir en la mayoría de los casos las líneas curvas por rectas. [[J. Massau]] generalizó este principio hacia [[1880]]. | ||
| + | |||
[[Maurice d'Ocagne]] reemplazó en [[1884]] los cuadriculados y sistemas de curvas por simples escalas graduadas, rectas o curvas, gracias a su concepción de los puntos isópletos. Posteriormente sistematizó todos estos métodos dispersos en un cuerpo definitivo de doctrina, a la que llamó [[nomografía]]. | [[Maurice d'Ocagne]] reemplazó en [[1884]] los cuadriculados y sistemas de curvas por simples escalas graduadas, rectas o curvas, gracias a su concepción de los puntos isópletos. Posteriormente sistematizó todos estos métodos dispersos en un cuerpo definitivo de doctrina, a la que llamó [[nomografía]]. | ||
| + | |||
Los nomogramas tuvieron un gran desarrollo en los tres primeros cuartos del [[siglo XX]], tanto en ingeniería civil como en las ramas de [[química]], [[eléctrica]], [[electrónica]] e [[aeronáutica]]. Fueron incluidos en los manuales de las disciplinas y además se publicaron colecciones separadas de ellos. Su limitada precisión, de dos o tres cifras significativas, restringe en cambio su uso en campos como la [[astronomía]] o el cálculo financiero, en los que la exactitud tiene importancia primordial. | Los nomogramas tuvieron un gran desarrollo en los tres primeros cuartos del [[siglo XX]], tanto en ingeniería civil como en las ramas de [[química]], [[eléctrica]], [[electrónica]] e [[aeronáutica]]. Fueron incluidos en los manuales de las disciplinas y además se publicaron colecciones separadas de ellos. Su limitada precisión, de dos o tres cifras significativas, restringe en cambio su uso en campos como la [[astronomía]] o el cálculo financiero, en los que la exactitud tiene importancia primordial. | ||
| + | |||
El perfeccionamiento y la popularización de las calculadoras y [[ordenadores electrónicos]] en el último cuarto del [[siglo XX]] significó la práctica desaparición de los nomogramas, al facilitar enormemente la realización completa de cálculos exactos que el operador no sabría ni siquiera plantear por sí mismo. Los nomogramas empero siguen teniendo actualmente la misma utilidad de siempre y presentan algunas ventajas específicas que no eran desconocidas para sus inventores, como es la captación sinóptica del rango de valores que puede adoptar la solución de un problema, la presentación de la estructura de las relaciones que se dan entre sus parámetros o la posibilidad de ser utilizados en casi cualquier circunstancia imaginable. | El perfeccionamiento y la popularización de las calculadoras y [[ordenadores electrónicos]] en el último cuarto del [[siglo XX]] significó la práctica desaparición de los nomogramas, al facilitar enormemente la realización completa de cálculos exactos que el operador no sabría ni siquiera plantear por sí mismo. Los nomogramas empero siguen teniendo actualmente la misma utilidad de siempre y presentan algunas ventajas específicas que no eran desconocidas para sus inventores, como es la captación sinóptica del rango de valores que puede adoptar la solución de un problema, la presentación de la estructura de las relaciones que se dan entre sus parámetros o la posibilidad de ser utilizados en casi cualquier circunstancia imaginable. | ||
Revisión del 10:46 6 dic 2011
| ||||||
Nomograma. ábaco o nomografo .Es un instrumento gráfico de cálculo, un diagrama bidimensional que permite el cómputo gráfico y aproximado de una función de cualquier número de variables. En su concepción más general, el nomograma representa simultáneamente el conjunto de las ecuaciones que definen determinado problema y el rango total de sus soluciones.
Definición
Es un modelo que utiliza un algorritmo o una fórmula matemática para predecir la probabilidad de un resultado, optimizado para una mayor seguridad predictiva. Los nomogramas son una herramienta de uso cotidiano.Una de sus ventajas es su utilidad para realizar la síntesis de cuadros complejos en el momento de satisfacer todas las inquietudes de los pacientes.
Por ejemplo en la práctica diaria se asiste a pacientes que exigen un mayor caudal de información sobre la enfermedad que motiva su consulta.Muchas veces demuestran que han leído suficientemente sobre el tema, exponen sus dudas respecto del pronóstico y exigen certezas sobre el tratamiento que el profesional sugiere.
Esto obliga a todos los médicos a estar permanentemente actualizados, ya sea por medio de revistas, libros de textos, cursos, congresos o a través de la enorme cantidad de información médica que se encuentra en Internet.Y toda esta información debe ser resumida para que sea entendible. Esto puede hacerse con nomogramas.
Ademas se trata de un instrumento de cálculo analógico, como lo es la regla de cálculo, por utilizar segmentos continuos de líneas para representar los valores numéricos discretos que pueden asumir las variables. Los nomogramas solían utilizarse en casos en que la obtención de una respuesta exacta era imposible o muy inconveniente, mientras que la obtención de una solución aproximada era suficiente y muy deseable.
Las tablas
Los nomogramas están íntimamente relacionados con otro instrumento tradicional de solución de problemas y de presentación sucinta de información científica, las tablas. Como decía en 1911 el ingeniero militar español Ricardo Seco, "si fuese posible reunir en un pequeño volumen una colección de tablas donde se hallasen consignados los resultados que dan las fórmulas de más frecuente aplicación para todos los valores que en la práctica pueden tomar las distintas variables que contienen, se habría llegado al desideratum que debe tratar de llenar todo manual de carácter práctico."
Pero, añadía, "tal colección de tablas es irrealizable porque, descontado el excesivo trabajo, largo tiempo necesario para su construcción y gran volumen que ocuparían," si existiesen más de tres variables en la fórmula "no hay medio práctico de construirlas". En cambio, como ha quedado dicho, las técnicas nomográficas permiten construir nomogramas de prácticamente cualquier número de variables.
D'Ocagne afirmaba en Le calcul simplifié que "los nomogramas pueden considerarse como tablas de cálculos completos", añadiendo a las ventajas ya mencionadas que tienen sobre ellas la facilidad de interpolación visual, al tiempo que reconocía el inconveniente de que la precisión que pueden alcanzar los datos de las tablas es en principio tan grande como se quiera, mientras que la de los nomogramas es esencialmente muy limitada.
Su Uso
Al ser un nomograma la representación gráfica de una ecuación de varias variables, ha de constar de tantos elementos gráficos como variables tenga la ecuación. Estos elementos serán puntos o líneas, rectas o curvas, según los casos. Dados los valores de todas las variables menos una, el de esta última puede encontrarse por medio de algún recurso geométrico inmediato (que generalmente es el trazado de otra línea que pasa por ese punto).
Por tanto, el nomograma de una ecuación de dos variables (y = f(x)) tendrá dos elementos gráficos, normalmente dos rectas graduadas, o escalas, dispuestas de tal modo que la determinación del valor de una de las variables (fijación de un punto de la línea) especifique el valor de la otra, la desconocida o función. El nomograma de una ecuación de tres variables (z = f(x, y)) constará normalmente de tres escalas y así sucesivamente.
El arte de la nomografía consiste precisamente en elaborar dichas escalas y disponerlas en el plano de tal manera que el trazado de líneas rectas que las atraviesen determine los puntos colineares existentes en cada una de las escalas, puntos que representarán los distintos valores relacionados por la función en cada caso concreto.
La disposición relativa entre estos elementos, en cambio, no puede predecirse, pues vendrá determinada por la naturaleza del problema en cuestión o por otro tipo de consideraciones. Por ejemplo, el nomograma de la función de dos variables que relaciona los grados Celsius de temperatura con los Farenheit puede consistir en dos escalas paralelas adecuadamente situadas. Para utilizarlo bastará con colocar una regla perpendicular a la escala que contenga el dato conocido; el otro se encontrará en el punto en que la regla corte a su escala correspondiente.
Pero es evidente que el espacio que separa ambas escalas no desempeña ninguna función especial, por lo que se le puede reducir progresivamente hasta el extremo de hacerlo desaparecer y que ambas se confundan en una sola, que quedará así rotulada a ambos lados, siendo entonces inmediata la lectura del resultado de la conversión.
Ejemplos de nomograma
- Nomograma en espiral -- la espiral de Cornu.
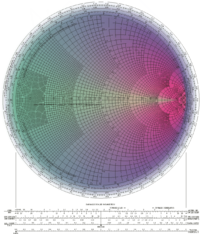
- La carta de Smith, reproducida al inicio del artículo, que se utiliza en electrónica y en análisis de sistemas.
- papel reticulado - semilogarítmico, doblemente logarítmico, probabilístico, destinados todos ellos a representar como líneas rectas diversas funciones no lineales.
Un gráfico útil Para reducir el volumen del aire medido en ATPS se utilizará la expresión Volumen aire STPD - (Volumen aire ATPS),(Factor STPD). Nota: Los valores del factor STPD empiezan en 0.570 y así en orden progresivo hasta 1.020 (ejemplo: 0.750)
Historia
Los astrolabios, cuadrantes y sectores de finales de la Edad Media y del Renacimiento (colectivamente llamados instrumentos matemáticos) ya estaban destinados a resolver problemas prácticos de índole matemática de forma gráfica y mecánica. La invención de la escala de Gunter en el siglo XVII constituyó la primera representación gráfica de una función mediante una escala graduada y fue esencial para todos los avances posteriores. Otro paso decisivo fue la invención por Descartes de la geometría analítica, que permite la representación gráfica de cualquier función matemática por medio de una curva.
Fueron especialmente los ingenieros militares y otros funcionarios públicos, encargados de resolver regularmente problemas cuantitativos de carácter repetitivo, quienes mostraron naturalmente mayor interés en procurarse ayudas para su tarea. Así L. Pouchet publicó en 1797 una obra titulada Métrologie terrestre, que contiene un apéndice designado Arithmétique linéaire en el que se contiene el primer intento sistemático de construcción de tablas gráficas de doble entrada.
En 1842 Léon Lalanne propuso el empleo de dispositivos de este género para el cálculo de desmontes y terraplenes y en 1843 formuló el principio de anamorfosis, que facilitó mucho la construcción de estos gráficos de doble entrada, a los que llamó ábacos, al sustituir en la mayoría de los casos las líneas curvas por rectas. J. Massau generalizó este principio hacia 1880.
Maurice d'Ocagne reemplazó en 1884 los cuadriculados y sistemas de curvas por simples escalas graduadas, rectas o curvas, gracias a su concepción de los puntos isópletos. Posteriormente sistematizó todos estos métodos dispersos en un cuerpo definitivo de doctrina, a la que llamó nomografía.
Los nomogramas tuvieron un gran desarrollo en los tres primeros cuartos del siglo XX, tanto en ingeniería civil como en las ramas de química, eléctrica, electrónica e aeronáutica. Fueron incluidos en los manuales de las disciplinas y además se publicaron colecciones separadas de ellos. Su limitada precisión, de dos o tres cifras significativas, restringe en cambio su uso en campos como la astronomía o el cálculo financiero, en los que la exactitud tiene importancia primordial.
El perfeccionamiento y la popularización de las calculadoras y ordenadores electrónicos en el último cuarto del siglo XX significó la práctica desaparición de los nomogramas, al facilitar enormemente la realización completa de cálculos exactos que el operador no sabría ni siquiera plantear por sí mismo. Los nomogramas empero siguen teniendo actualmente la misma utilidad de siempre y presentan algunas ventajas específicas que no eran desconocidas para sus inventores, como es la captación sinóptica del rango de valores que puede adoptar la solución de un problema, la presentación de la estructura de las relaciones que se dan entre sus parámetros o la posibilidad de ser utilizados en casi cualquier circunstancia imaginable.
Fuentes
- [www.definition-of.net/ definicion-de-nomograma]
- [www.docmedical.com/ sup/nomogramas.ppt]
- [www.definicion.org/ nomograma]
- [www.docmedical.com/ sup/nomogramas.ppt]
- materias/Metalurgica_de_la_soldadura/Archivos%20de%20Metsold/U4-%203-metodos%20para%20calculo%20TEMP%20precalentamiento-09.pdf
- file.php/1096/Folleto_de_Tablas_y_Nomogramas_de_Ergonomia/Nomograma_Sup_Cutanea_Folleto_SI.doc
- [1]