Velocidad angular

Velocidad angular. Concepto: La rapidez, con que cambia de posición un cuerpo o con que recorre el ángulo barrido por el radio en la unidad de tiempo.

En el movimiento circular, se denomina velocidad angular a la magnitud que caracteriza la rapidez con que varía el ángulo barrido por la línea que une la partícula que gira con el centro de rotación.

Representación

Se representa comúnmente con la letra griega omega (ω) y se expresa en radianes/segundo (rad/s)

Otra denominación

La velocidad angular también es conocida en física como frecuencia cíclica.

Para un objeto que gira alrededor de un eje, cada punto del objeto tiene la misma velocidad angular o para el movimiento circular uniforme, la velocidad angular es constante y se calcula mediante la fórmula:

ω= 2π/T, donde T es el período de rotación.

Por otra parte, como el período T = 1/f, donde f es la frecuencia de rotación, entonces la velocidad angular también puede ser escrita por la relación:

ω= 2πf

Ejemplo

Representación de las tres magnitudes vectoriales(velocidad angular, radio vector y velocidad lineal)

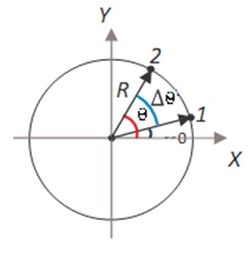
Cuando un móvil describe una trayectoria circular de centro O, su posición en cualquier instante viene dada por el vector de posición, r, y el ángulo, θ, formado por este vector y otra recta de referencia fija en el espacio. Su velocidad angular, ω, está representada por un vector axial cuyo módulo es dθ/dt, su dirección es perpendicular en O al plano de giro y cuyo sentido viene dado, en función del sentido de giro, por la regla de la mano derecha.

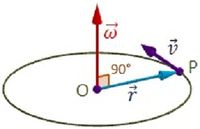
Cuando un sólido gira sin deslizar alrededor de un eje fijo, los puntos situados en el eje son fijos, mientras que el resto de los puntos están animados de movimientos circulares cuyos centros se encuentran en el eje. Cada uno de estos puntos posee una velocidad lineal distinta, v, pero la velocidad angular de todos ellos es común, ω, y es la velocidad angular de rotación del sólido alrededor del eje.

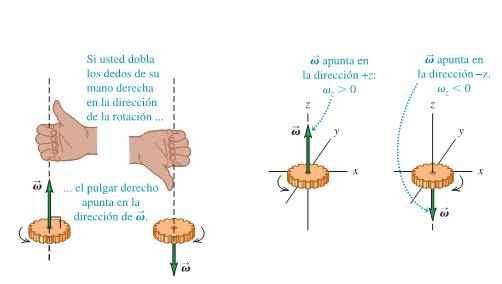
Determinación de la dirección del vector velocidad angular

Para determinar la dirección del vector velocidad angular se utiliza la Regla de la mano derecha según se muestra en la imagen:

Si se invierte el sentido de la rotación, se invierte la dirección del vector

Fuente

• Resnick,Robert & Krane, Kenneth S. (2001). Physics (en inglés). New York: John Wiley & Sons. ISBN 0-471-32057-9.
• Ortega, Manuel R. (1989-2006). Lecciones de Física (4 volúmenes). Monytex. ISBN 84-404-4290-4, ISBN 84-398-9218-7, ISBN 84-398-9219-5, ISBN 84-604-4445-7. Consultado el 26 de junio del 2017 de Wikipedia portable del 2016.
• Serway, Raymond A.; Jewett, John W. (2004). Physics for Scientists and Engineers (en inglés) (6ª edición). Brooks/Cole. ISBN 0-534-40842-7. Consultado el 26 de junio del 2017 de Wikipedia portable del 2016.
• Tipler, Paul A. (2000). Física para la ciencia y la tecnología (2 volúmenes). Barcelona: Ed. Reverté. ISBN 84-291-4382-3.
• Velocidad angular del planeta Tierra, Consultado de la Red C.U.B.A el 29 de Junio de 2017
• Sears-Zemansky (Volumen1), página 288. Física Universitaria. ISBN 978-607-442-288-7
• Velocidad angular

Categorías: