Diferencia entre revisiones de «Lenguaje regular»
(→Definiciones.) |
m (Texto reemplazado: «<div align="justify">» por «») |
||
| (No se muestra una edición intermedia de otro usuario) | |||
| Línea 1: | Línea 1: | ||
{{Definición|nombre=Lenguaje regular|imagen=Jerarquia_Chomsky_A.gif|concepto=Según la [[jerarquía de Chomsky]] son los lenguajes de tipo 3, reconocibles con [[Autómata finito|autómatas finitos]].}} | {{Definición|nombre=Lenguaje regular|imagen=Jerarquia_Chomsky_A.gif|concepto=Según la [[jerarquía de Chomsky]] son los lenguajes de tipo 3, reconocibles con [[Autómata finito|autómatas finitos]].}} | ||
| − | + | ||
'''Lenguaje regular'''. En [[Lingüística]], [[Matemáticas]] e [[Informática]] y en la [[jerarquía de Chomsky]] se refiere a los lenguajes de tipo 3, aquellos que pueden representarse mediante [[Gramática regular|gramáticas regulares]], [[Autómata finito|autómatas finitos]] o [[Expresión regular|expresiones regulares]]. | '''Lenguaje regular'''. En [[Lingüística]], [[Matemáticas]] e [[Informática]] y en la [[jerarquía de Chomsky]] se refiere a los lenguajes de tipo 3, aquellos que pueden representarse mediante [[Gramática regular|gramáticas regulares]], [[Autómata finito|autómatas finitos]] o [[Expresión regular|expresiones regulares]]. | ||
| Línea 25: | Línea 25: | ||
==Ejemplo 1.== | ==Ejemplo 1.== | ||
| − | Demuestre que el lenguaje conformado por los nombres de [[variable|variables]] de | + | Demuestre que el lenguaje conformado por los nombres de [[variable|variables]] de PROLOG es un lenguaje regular. |
Primero debe recordarse que un nombre de variable PROLOG viene dada por la forma: | Primero debe recordarse que un nombre de variable PROLOG viene dada por la forma: | ||
| − | '' | + | ''Cualquier palabra que comience con una letra mayúscula seguida o no de combinaciones de letras, cifras o subrayados o que comience con al menos un subrayado seguido o no de cualquier secuencia de alfanuméricos o subrayados''. |
Cada de las siguientes construcciones son equivalentes en virtud de la definición dada antes: | Cada de las siguientes construcciones son equivalentes en virtud de la definición dada antes: | ||
| Línea 43: | Línea 43: | ||
La existencia y formalización de los lenguajes regulares (LR) y su vinculación con otros artefactos lingüísticos-matemáticos ya bien formalizados, estudiados e incluso llevados a la práctica ha sido de vital importancia en el ulterior desarrollo de los mecanismos de procesamiento de lenguajes de computadora, fundamentalmente en los analizadores lexicográficos gracias a la posibilidad de derivar el reconocimiento de los LR mediante autómatas finitos que son fáciles de implementar computacionalmente con mecanismos simples y rápidos, óptimos en la obtención de ''parsers'' veloces y robustos que a su vez le ofrecen a los desarrolladores información detallada de los errores léxicos, sintácticos e incluso advierten sobre errores semánticos. | La existencia y formalización de los lenguajes regulares (LR) y su vinculación con otros artefactos lingüísticos-matemáticos ya bien formalizados, estudiados e incluso llevados a la práctica ha sido de vital importancia en el ulterior desarrollo de los mecanismos de procesamiento de lenguajes de computadora, fundamentalmente en los analizadores lexicográficos gracias a la posibilidad de derivar el reconocimiento de los LR mediante autómatas finitos que son fáciles de implementar computacionalmente con mecanismos simples y rápidos, óptimos en la obtención de ''parsers'' veloces y robustos que a su vez le ofrecen a los desarrolladores información detallada de los errores léxicos, sintácticos e incluso advierten sobre errores semánticos. | ||
| − | Lo mismo sucede por ejemplo con las expresiones regulares implementadas ya en muchos | + | Lo mismo sucede por ejemplo con las expresiones regulares implementadas ya en muchos Lenguaje de programación de propósito general modernos que permiten a los desarrolladores de lenguajes mecanismos muy eficientes para la obtención intuitiva de partes de compiladores que reconocen los ''tókenes'' o partículas lexicales del [[código fuente]] como fase del proceso completo de interpretación o compilado, según sea el caso. |
| − | A manera de ilustración en el caso del ejemplo anterior vemos la siguiente | + | A manera de ilustración en el caso del ejemplo anterior vemos la siguiente función Python que a partir de cualquiera de los elementos formalizadores del LR correspondiente permite decidir si un texto ''w'' es una variable PROLOG: |
<pre> | <pre> | ||
| Línea 68: | Línea 68: | ||
Pero el alcance de los LR no se queda en el mundo de la [[compilación]] de lenguajes de ordenador como se ve en el siguiente ejemplo. | Pero el alcance de los LR no se queda en el mundo de la [[compilación]] de lenguajes de ordenador como se ve en el siguiente ejemplo. | ||
| − | ===Ejemplo 2 | + | ===Ejemplo 2=== |
En un acuario de [[Miami]] se entrenan las capacidades intelectuales de los [[Delfín|delfines]] en cautiverio y tiene especial importancia los resultados que tiene uno de los ejemplares quien ha aprendido a reconocer cantidades pares a partir de imagenes de peces, llegando a distinguir cuando hay un número par o no de peces en la imagen. Muestre que las imágenes de cantidad de peces pares es un lenguaje regular que puede percibir el delfín. | En un acuario de [[Miami]] se entrenan las capacidades intelectuales de los [[Delfín|delfines]] en cautiverio y tiene especial importancia los resultados que tiene uno de los ejemplares quien ha aprendido a reconocer cantidades pares a partir de imagenes de peces, llegando a distinguir cuando hay un número par o no de peces en la imagen. Muestre que las imágenes de cantidad de peces pares es un lenguaje regular que puede percibir el delfín. | ||
| Línea 85: | Línea 85: | ||
* [[Lenguaje libre de contexto]]. | * [[Lenguaje libre de contexto]]. | ||
| − | ==Fuentes | + | ==Fuentes== |
| − | + | *Tanembaum, A. Compilers: Principles, Tecniques, and Tools. Tomo 1. ACM Press. 5ta Edición. | |
| − | + | *Conferencias de la Asignatura "Compilación 1" del Departamento de Ciencias de la Computación de la Universidad de Oriente de la [[Universidad de Oriente]]. [[Santiago de Cuba]], [[2000]]. | |
| − | + | *Artículo [http://es.wikipedia.org/wiki/Lenguaje_regular Lenguajes regulares]. Consultado el [[23 de febrero]] de [[2012]]. | |
| + | |||
| − | |||
[[Categoría:Lingüística]][[Categoría:Matemáticas]][[Categoría:Informática]] | [[Categoría:Lingüística]][[Categoría:Matemáticas]][[Categoría:Informática]] | ||
última versión al 15:30 6 jul 2019
| ||||||
Lenguaje regular. En Lingüística, Matemáticas e Informática y en la jerarquía de Chomsky se refiere a los lenguajes de tipo 3, aquellos que pueden representarse mediante gramáticas regulares, autómatas finitos o expresiones regulares.
Son los lenguajes formales más simples, con los mecanismos de representación y reconocimiento más estudiados. Su aplicación práctica en la teoría y construcción de intérpretes y compiladores de lenguajes de programación o de especificación o formato de información, especialmente como microcomponentes del analizador lexicográfico que detecta los tókenes como constantes numéricas, cadenas de texto, operadores, palabras reservadas (keywords), separadores, etc. Pero también se puede apreciar su uso en máquinas expendedoras, teléfonos públicos, calculadoras y otros artefactos electromecánicos.
Sumario
Definiciones.
Se dice que un lenguaje es regular si y sólo si se cumple cualquiera de las siguientes proposiciones:
- Tiene al menos una gramática regular G que lo produce.
- Puede ser reconocido por un autómata finito A.
- Existe una expresión regular Er que representa a todas las cadenas de L.
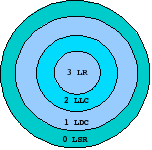
Dentro de la Jerarquía de Chomsky se refiere a los lenguajes de tipo 3, el subconjunto de lenguajes formales mas restringido dentro de la jerarquía, como se ve en la imagen.
También puede realizarse una definición recursiva-constructiva de los lenguajes regulares mediante el álgebra de lenguajes formales.
Un lenguaje regular sobre un alfabeto T ó LR(T) es:
- El lenguaje vacío {}.
- El lenguaje conformado por la cadena vacía
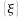 o lenguaje trivial.
o lenguaje trivial. - Un lenguaje {x} conformado por un único símbolo x de T.
- Si A y B son lenguajes regulares sobre T, entonces AB (Concatenación de lenguajes),
 (Unión de lenguajes), A* (Clausura de lenguaje o Estrella de Kleene) son también lenguajes regulares sobre T.
(Unión de lenguajes), A* (Clausura de lenguaje o Estrella de Kleene) son también lenguajes regulares sobre T. - Cualquier otro lenguaje que pueda obtenerse a partir de 1 a 4.
Ejemplo 1.
Demuestre que el lenguaje conformado por los nombres de variables de PROLOG es un lenguaje regular.
Primero debe recordarse que un nombre de variable PROLOG viene dada por la forma:
Cualquier palabra que comience con una letra mayúscula seguida o no de combinaciones de letras, cifras o subrayados o que comience con al menos un subrayado seguido o no de cualquier secuencia de alfanuméricos o subrayados.
Cada de las siguientes construcciones son equivalentes en virtud de la definición dada antes:
- La expresión regular (A|B|...|Z)|_(A|B|...|Z|a|b|...|z|_)*.
- El siguiente autómata finito representado como diagrama de estados permite el reconocimiento de variables de PROLOG.
- Una gramática con producciones de la forma:
Importancia de los lenguajes regulares.
La existencia y formalización de los lenguajes regulares (LR) y su vinculación con otros artefactos lingüísticos-matemáticos ya bien formalizados, estudiados e incluso llevados a la práctica ha sido de vital importancia en el ulterior desarrollo de los mecanismos de procesamiento de lenguajes de computadora, fundamentalmente en los analizadores lexicográficos gracias a la posibilidad de derivar el reconocimiento de los LR mediante autómatas finitos que son fáciles de implementar computacionalmente con mecanismos simples y rápidos, óptimos en la obtención de parsers veloces y robustos que a su vez le ofrecen a los desarrolladores información detallada de los errores léxicos, sintácticos e incluso advierten sobre errores semánticos.
Lo mismo sucede por ejemplo con las expresiones regulares implementadas ya en muchos Lenguaje de programación de propósito general modernos que permiten a los desarrolladores de lenguajes mecanismos muy eficientes para la obtención intuitiva de partes de compiladores que reconocen los tókenes o partículas lexicales del código fuente como fase del proceso completo de interpretación o compilado, según sea el caso.
A manera de ilustración en el caso del ejemplo anterior vemos la siguiente función Python que a partir de cualquiera de los elementos formalizadores del LR correspondiente permite decidir si un texto w es una variable PROLOG:
def variablePROLOG(w):
'''(str)-->bool. True si "w" es un nombre de variable correcto'''
if (w[0].isalpha and w[0]==w[0].upper()) or w[0]=='_':
#El primer caracter es una mayuscula o un subrayado
w = w[1:] #Se quita el primer caracter
while w and (w[0].isalnum() or w[0]=='_'):
#Mientras queden caracteres en "w" y el primer caracter actual sea un alfanumerico o un subrayado, todo esta bien
w = w[1:] #Quitar el primer caracter
if w=='':
#Si ya no quedan elementos a revisar, es una variable PROLOG
return True
return False
Varias funciones de esa naturaleza componen los analizadores lexicográficos para discriminar la función de cada token del lenguaje en cuestión: constante númerica, literal de cadena de texto, identificador, separador, etc.; según sea el caso.
Y también puede verse que existe una estrecha relación en cómo implementar las funciones reconocedoras de LR y la expresión o la gramática regulares o el autómata finito correspondiente, al punto que desde hace más de 3 décadas existen aplicaciones generadoras de analizadores lexicográficos como el Flex o el Bisonte.
Pero el alcance de los LR no se queda en el mundo de la compilación de lenguajes de ordenador como se ve en el siguiente ejemplo.
Ejemplo 2
En un acuario de Miami se entrenan las capacidades intelectuales de los delfines en cautiverio y tiene especial importancia los resultados que tiene uno de los ejemplares quien ha aprendido a reconocer cantidades pares a partir de imagenes de peces, llegando a distinguir cuando hay un número par o no de peces en la imagen. Muestre que las imágenes de cantidad de peces pares es un lenguaje regular que puede percibir el delfín.
Se define a cada pez de las imágenes con la letra p minúscula y se ve que para las imagenes pares puede definirse las siguientes producciones de una gramática regular:
Por ende, se trata de un LR.
Véase también.
- Gramática regular.
- Autómata finito.
- Expresión regular.
- Flex.
- Jerarquía de Chomsky.
- Lenguaje libre de contexto.
Fuentes
- Tanembaum, A. Compilers: Principles, Tecniques, and Tools. Tomo 1. ACM Press. 5ta Edición.
- Conferencias de la Asignatura "Compilación 1" del Departamento de Ciencias de la Computación de la Universidad de Oriente de la Universidad de Oriente. Santiago de Cuba, 2000.
- Artículo Lenguajes regulares. Consultado el 23 de febrero de 2012.