Diferencia entre revisiones de «Función lineal»
(→Características generales) |
(→En la economía: función constante) |
||
| (No se muestran 5 ediciones intermedias de 4 usuarios) | |||
| Línea 16: | Línea 16: | ||
La pendiente es la inclinación de la recta con respecto al eje de abscisas. | La pendiente es la inclinación de la recta con respecto al eje de abscisas. | ||
| − | Si m | + | Si m > 0, la recta se inclina hacia arriba, la función es creciente y el ángulo que forma la recta con la parte positiva del eje OX es agudo. |
[[Image:FL11.JPG]] | [[Image:FL11.JPG]] | ||
| − | Si m | + | Si m < 0, la recta se inclina hacia abajo, la función es decreciente y el ángulo que forma la recta con la parte positiva del eje OX es obtuso. |
[[Image:FL22.JPG]] | [[Image:FL22.JPG]] | ||
| Línea 32: | Línea 32: | ||
La pendiente m de la recta que pasa por los punto P1(x1; y1) y P2(x2; y2) se calcula por la fórmula | La pendiente m de la recta que pasa por los punto P1(x1; y1) y P2(x2; y2) se calcula por la fórmula | ||
| − | [[Image:Pendiente.JPG|border|Pendiente.JPG]] | + | [[Image:Pendiente.JPG|border|Pendiente.JPG]] |
=== Cero de la función === | === Cero de la función === | ||
| Línea 39: | Línea 39: | ||
El elemento del dominio de la función lineal f(x) = mx + n (m ≠0) cuya imagen es cero, se denomina cero de esta función. | El elemento del dominio de la función lineal f(x) = mx + n (m ≠0) cuya imagen es cero, se denomina cero de esta función. | ||
| + | ==Usos diversos== | ||
| + | ===En la física=== | ||
| + | * x = vt + x<sub>0</sub>, representa el espacio x recorrido por un móvil, a una velocidad constante v, durante el tiempo t que parte del punto que dista x<sub>0</sub>, del origen de coordenadas. En este caso x = f(t). | ||
| + | ===En la economía=== | ||
| + | # Si un pasajero gasta diariamente en pasaje p pesos, al cabo de x días habrá gastado la suma y = px. | ||
| + | # En un cierto país a cada trabajador estatal le dan un aguinaldo de 300 unidades monetarias por Año nuevo, sea x el entero positivo que identifica al trabajador en una lista oficial. Se formula la función f(x) = 300, que es un caso de función constante para valores enteros. | ||
=== Ejercicios: === | === Ejercicios: === | ||
| Línea 54: | Línea 60: | ||
b) Si la relación que se establece entre los elementos de dos conjuntos no constituye una correspondencia, entonces: | b) Si la relación que se establece entre los elementos de dos conjuntos no constituye una correspondencia, entonces: | ||
| + | |||
___ es función. | ___ es función. | ||
| + | |||
___ no es función. | ___ no es función. | ||
| + | |||
___ no se puede decidir. | ___ no se puede decidir. | ||
| − | c) Si en una correspondencia, están asociados todos los elementos del | + | c) Si en una correspondencia, están asociados todos los elementos del conjunto de llegada, con elementos del conjunto de partida, entonces: |
___ es función. | ___ es función. | ||
| Línea 66: | Línea 75: | ||
___ no se puede decidir. | ___ no se puede decidir. | ||
| − | d) Si al menos un elemento del | + | d) Si al menos un elemento del conjunto de llegada de una correspondencia, está asociado, entonces: |
| + | |||
___ es función. | ___ es función. | ||
| + | |||
___ no es función. | ___ no es función. | ||
| + | |||
___ no se puede decidir. | ___ no se puede decidir. | ||
| − | e) Si los elementos asociados del | + | |
| + | e) Si los elementos asociados del conjunto de llegada de una correspondencia, lo hacen cada uno con un único elemento del conjunto de partida, entonces: | ||
___ es función. | ___ es función. | ||
| Línea 78: | Línea 91: | ||
___ no se puede decidir. | ___ no se puede decidir. | ||
| − | f) Si cada uno de los elementos del | + | f) Si cada uno de los elementos del conjunto de partida de una correspondencia, está asociado con un único elemento del conjunto de llegada, entonces: |
| + | |||
___ es función. | ___ es función. | ||
| + | |||
___ no es función. | ___ no es función. | ||
| + | |||
___ no se puede decidir. | ___ no se puede decidir. | ||
| + | |||
g) Si la relación que se establece entre los elementos de dos conjuntos representa una función, entonces: | g) Si la relación que se establece entre los elementos de dos conjuntos representa una función, entonces: | ||
| Línea 106: | Línea 123: | ||
Complete las siguientes situaciones de manera que obtengas una proposición verdadera: | Complete las siguientes situaciones de manera que obtengas una proposición verdadera: | ||
| − | a) | + | a) La imagen del argumento –2 es ___ |
| − | b) | + | b) 2 es la imagen del argumento ___ |
| − | c) | + | c) -1 es pre–imagen de ___ |
| − | d) | + | d) 0 es imagen de ___ |
| − | e) | + | e) La imagen de 2 es ___ |
| − | f) | + | f) La imagen de un elemento cualquiera x es ___. |
| − | g) | + | g) Marque con una “x” la ecuación que consideres define a la función descrita: |
____ y= x + 2 ____ y= -x + 2 ____ y= 2x ____ y= -2x ____ y= x/2. | ____ y= x + 2 ____ y= -x + 2 ____ y= 2x ____ y= -2x ____ y= x/2. | ||
g) Explique a un compañero cómo procedió en el inciso f). | g) Explique a un compañero cómo procedió en el inciso f). | ||
| + | |||
4- ¿Cuáles de las siguientes ecuaciones definen una función lineal?. Justifique en cada caso: | 4- ¿Cuáles de las siguientes ecuaciones definen una función lineal?. Justifique en cada caso: | ||
| Línea 154: | Línea 172: | ||
7- Dada la función f(x)= 2x + 2 | 7- Dada la función f(x)= 2x + 2 | ||
| − | I. | + | I. Determine el valor de x para el cual: |
a) f(x)= 4 b) f(x)= -8 c) f(x)= 0 | a) f(x)= 4 b) f(x)= -8 c) f(x)= 0 | ||
| − | II. | + | II. ¿Cuál es el cero de f(x)?. ¿Por qué?. |
| − | III. | + | III. Represente gráficamente estas funciones. |
8- Determine los ceros de las siguientes funciones lineales: | 8- Determine los ceros de las siguientes funciones lineales: | ||
| Línea 166: | Línea 184: | ||
a) f(x)= x + 2 b) h(x)= 2x + 4 c) y= -3x – 1 d) y= 3 | a) f(x)= x + 2 b) h(x)= 2x + 4 c) y= -3x – 1 d) y= 3 | ||
| − | I. | + | I. Escribe en cada caso el par ordenado correspondiente. |
| − | II. | + | II. Represente las funciones gráficamente. |
== Fuente == | == Fuente == | ||
última versión al 00:18 22 ago 2019
| ||||||
Función lineal. La función que a cada x€R le hace corresponder un número real f(x) = mx + n. Donde m y n son números reales dados, se denomina función lineal.
Sumario
Características generales
Una función lineal según la primera definición dada anteriormente representa una aplicación lineal si y sólo si n = 0. Así, algunos autores llaman función lineal a aquella de la forma mientras que llaman función afín a la que tiene la forma
, cuando n es distinto de cero. La grafica de la función lineal es una recta.
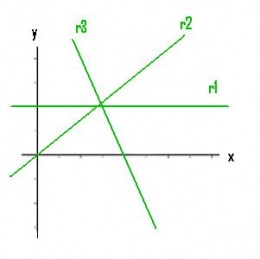
Los valores de m y n son constantes reales y x es una variable real. La constante m es la pendiente de la recta, y n es el punto de corte de la recta con el eje y. Cuando cambiamos m modificamos la inclinación de la recta y cuando cambiamos n desplazamos la línea arriba o abajo.
Pendiente
La pendiente es la inclinación de la recta con respecto al eje de abscisas.
Si m > 0, la recta se inclina hacia arriba, la función es creciente y el ángulo que forma la recta con la parte positiva del eje OX es agudo.
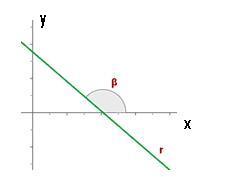
Si m < 0, la recta se inclina hacia abajo, la función es decreciente y el ángulo que forma la recta con la parte positiva del eje OX es obtuso.
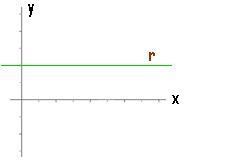
Si m = 0, la recta es paralela al eje x.
Calculo de la pendiente de la recta
La pendiente m de la recta que pasa por los punto P1(x1; y1) y P2(x2; y2) se calcula por la fórmula
Cero de la función
El dominio de la función lineal es el conjunto de los números reales.
El elemento del dominio de la función lineal f(x) = mx + n (m ≠0) cuya imagen es cero, se denomina cero de esta función.
Usos diversos
En la física
- x = vt + x0, representa el espacio x recorrido por un móvil, a una velocidad constante v, durante el tiempo t que parte del punto que dista x0, del origen de coordenadas. En este caso x = f(t).
En la economía
- Si un pasajero gasta diariamente en pasaje p pesos, al cabo de x días habrá gastado la suma y = px.
- En un cierto país a cada trabajador estatal le dan un aguinaldo de 300 unidades monetarias por Año nuevo, sea x el entero positivo que identifica al trabajador en una lista oficial. Se formula la función f(x) = 300, que es un caso de función constante para valores enteros.
Ejercicios:
1-Marque con una “X” lo que consideres correcto:
a) Si la relación que se establece entre los elementos de dos conjuntos constituye una correspondencia, entonces:
___ es función.
___ no es función.
___ no se puede decidir.
b) Si la relación que se establece entre los elementos de dos conjuntos no constituye una correspondencia, entonces:
___ es función.
___ no es función.
___ no se puede decidir.
c) Si en una correspondencia, están asociados todos los elementos del conjunto de llegada, con elementos del conjunto de partida, entonces:
___ es función.
___ no es función.
___ no se puede decidir.
d) Si al menos un elemento del conjunto de llegada de una correspondencia, está asociado, entonces:
___ es función.
___ no es función.
___ no se puede decidir.
e) Si los elementos asociados del conjunto de llegada de una correspondencia, lo hacen cada uno con un único elemento del conjunto de partida, entonces:
___ es función.
___ no es función.
___ no se puede decidir.
f) Si cada uno de los elementos del conjunto de partida de una correspondencia, está asociado con un único elemento del conjunto de llegada, entonces:
___ es función.
___ no es función.
___ no se puede decidir.
g) Si la relación que se establece entre los elementos de dos conjuntos representa una función, entonces:
___ es una correspondencia
___no es una correspondencia
___no se puede decidir
2- Escribe “V” si es verdadero y “F” si es falso. Justifica en cada caso.
En una función:
___ Todos los elementos del dominio están relacionados con elementos del conjunto imagen.
___ Todos los elementos del conjunto imagen están relacionados con elementos del dominio.
___ Dos elementos del dominio pueden estar relacionados con un mismo elemento del conjunto imagen.
___ Dos elementos del conjunto imagen pueden estar relacionados con un mismo elemento del dominio.
3- Una función numérica viene dada por la correspondencia siguiente: “A cada elemento del dominio se le asigna su duplo”.
Complete las siguientes situaciones de manera que obtengas una proposición verdadera:
a) La imagen del argumento –2 es ___
b) 2 es la imagen del argumento ___
c) -1 es pre–imagen de ___
d) 0 es imagen de ___
e) La imagen de 2 es ___
f) La imagen de un elemento cualquiera x es ___.
g) Marque con una “x” la ecuación que consideres define a la función descrita:
____ y= x + 2 ____ y= -x + 2 ____ y= 2x ____ y= -2x ____ y= x/2.
g) Explique a un compañero cómo procedió en el inciso f).
4- ¿Cuáles de las siguientes ecuaciones definen una función lineal?. Justifique en cada caso:
a) y= x2+2 b) y= 3x–4y c) p= 2m+5 d) y= 9 e) y= 2x+4
5- Clasifique las siguientes proposiciones en verdaderas o falsas. Justifique las falsas
a) __ El cero de la función f(x)=4x-8 es x = -2
b) __ La función f(x)=1/2x-5 es monótona creciente
c) __ La imagen de la función g(x)= -1/2x es el conjunto de los números reales.
d) __ La función h(x)=3x+5 corta el eje de las ¨ y ¨ en el punto (0;-5)
e) __ La función p(x)=5 es una recta paralela al eje ¨ y ¨
6- Dadas: g(x)= x – 1; h(x)= 5x; t(x)= -x – 1; v(x)= 5x - 10.
a) Determine en cada caso m y n.
b) Halle: g(1); h(0); t(-1); v(-2)
c) ¿Cuál es el valor de la imagen en cada uno de los casos del inciso b)?.
Nota: Al elemento del dominio cuya imagen es cero, se le llama cero de la función lineal.
d) ¿Cuál es el cero de cada una de las funciones g(x), h(x), t(x) y v(x)?.
7- Dada la función f(x)= 2x + 2
I. Determine el valor de x para el cual:
a) f(x)= 4 b) f(x)= -8 c) f(x)= 0
II. ¿Cuál es el cero de f(x)?. ¿Por qué?.
III. Represente gráficamente estas funciones.
8- Determine los ceros de las siguientes funciones lineales:
a) f(x)= x + 2 b) h(x)= 2x + 4 c) y= -3x – 1 d) y= 3
I. Escribe en cada caso el par ordenado correspondiente.
II. Represente las funciones gráficamente.
Fuente
- Baño Muñoz Félix. Colectivo de autores. Matemática 8vo grado.Editorial Pueblo y Educación. 1991.