Diferencia entre revisiones de «Relación binaria»

última versión al 15:14 2 oct 2020

Relación binaria
Concepto:	Sean A y B conjuntos no vacíos, se llama relación binaria a cualquier subconjunto del producto cartesiano AxB.

Relación binaria. Dícese en Matemática Discreta y Lógica de toda relación R que se establece entre los elementos de dos conjuntos no vacíos A y B y que se define mediante un conjunto de pares <x,y>, válidos para la propia relación con e y que indica.

Sumario

1 Definición
2 Ejemplos
3 Representación
4 Propiedades
- 4.1 Propiedades fundamentales de las relaciones binarias homogéneas.
5 Relaciones y funciones
6 Fuentes

Definición

Una relación binara R sobre A y B, conjuntos no vacíos, indicada como R_A,B, es un subconjunto de AxB. Formalmente hablando sería . Entonces, R_A,B es un conjunto de pares <x,y> con e .

A los conjuntos A y B se les conoce como conjunto de partida y conjunto de llegada. Al conjunto de elementos de A que aparecen en la relación se llama dominio y se representa Dom(R) . Al conjunto de elementos de B que aparecen en la relación se llama imagen y se representa Im(R) .

Evidentemente, también puede darse el caso A=B, donde la relación toma la forma . E

Las siguientes notaciones son válidas xRy, R(x,y), , Rxy(notación polaca) y se leen x relacionado con y según R.

Ejemplos

A={0, 1, 2, 3}, B={0, 1, 2, 3, 4, 5}, R_A,B={<0,1>, <0,2>, <0,3>, <0,4>, <0,5>, <1,2>, <1,3>, <1,4>, <1,5>, <2,3>, <2,4>, <2,5>, <3,4>, <3,5>}.
A={0, 1, 2, 3}, , R_A,B={<0,{}>, <1,{0}>, <1,{1}>, <1,{2}>, <1,{3}>, <2,{0,1}>, <2,{0,2}>, <2,{0,3}>, <3,{0,1,2}>, <3,{0,1,3}>, <3,{0,2,3}>, <3,{1,2,3}>}.
A={0,1,2,3}, R_A²=A²={<0, 0>, <0, 1>, <0, 2>, <0, 3>, <1, 0>, <1, 1>, <1, 2>, <1, 3>, <2, 0>, <2, 1>, <2, 2>, <2, 3>, <3, 0>, <3, 1>, <3, 2>, <3, 3>}.
A={0,1,2,3}, R_A²=A²={<0, 0>, <1, 1>, <2, 2>, <3, 3>}.
Sea C los siguientes cuerpos del Sistema Solar Interior: C={Sol, Mercurio, Venus, Tierra, Luna, Marte, Fobos, Deimos}, se define la relación x gira alrededor de y como G={<Mercurio, Sol>, <Venus, Sol>, <Tierra, Sol>, <Luna, Tierra>, <Marte, Sol>, <Fobos, Marte>, <Deimos, Marte>}.

Representación

Las relaciones binarias pueden representarse de manera explícita como vimos en los ejemplos anteriores o de forma implícita en tanto también son conjuntos. No obstante existen otras formas de representarlas que ayudan a visualizar de modo más fácil algunas propiedades que pueden caracterorarlas. Entre las más notables están la representación tabular y la del dígrafo asociado, por lo que en el último caso puede llegar a obtenerse un esquema gráfico de las relaciones.

Representación tabular

La representación tabular o matricial de las relaciones binarias es simple y sigue la siguiente estructura.

Sea R una relación binaria sobre A y B:

Se hace una tabla de n+1 filas por m+1 columnas, donde n es la cantidad de elementos de A y m, la de B.
En la celda superior izquierda se rotula el nombre de la relación R o un símbolo.
Se etiquetan y asocian los nombres de cada fila, a partir de la segunda, con cada elemento de A.
Se etiquetan y asocian los nombres de cada columna, a partir de la segunda, con cada elemento de B.
Para cada celda de la fila i, columna j: si iRj, se indica 1; de lo contrario, 0.

Dígrafo asociado

Sea R una relación binaria sobre A y B, se entiende por dígrafo asociado a R , al grafo orientado G=<A U B, R>; es decir, cuyos vértices serán los elementos de A y B y sus arcos, los pares pertenecientes a la relación en cuestión.

Ejemplos

Para el ejemplo 1, su representación tabular es:

R	1	2	3	4	5
0	1	1	1	1	1
1	0	1	1	1	1
2	0	0	1	1	1
3	0	0	0	1	1

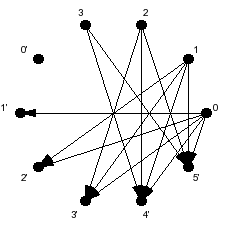
El dígrafo asociado:

G = <{0,0',1,1',2,2',3,3',4',5'}, {<0,1'>, <0,2'>, <0,3'>, <0,4'>, <0,5'>, <1,2'>, <1,3'>, <1,4'>, <1,5'>, <2,3'>, <2,4'>, <2,5'>, <3,4'>, <3,5'>}>.

Y su representación gráfica:

Nótese que a los elementos del conjunto B se les agregó un apóstrofo para distinguirlos de los que son iguales en el A.

Ejemplo 2:

R	{}	{0}	{1}	{2}	{3}	{0,1}	{0,2}	{0,3}	{1,2}	{1,3}	{2,3}	{0,1,2}	{0,1,3}	{0,2,3}	{1,2,3}
0	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0
1	0	1	1	1	1	0	0	0	0	0	0	0	0	0	0
2	0	0	0	0	0	1	1	1	1	1	1	0	0	0	0
3	0	0	0	0	0	0	0	0	0	0	0	1	1	1	1

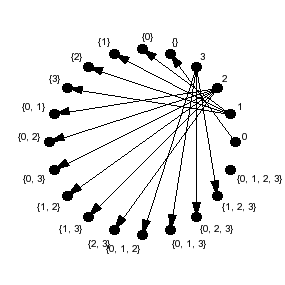
El dígrafo asociado:

G = <{0, 1, 2, 3, {}, {0}, {1}, {2}, {3}, {0,1}, {0,2}, {0,3}, {1,2}, {1,3}, {2,3}, {0,1,2}, {0,1,3}, {0,2,3}, {1,2,3}, {0,1,2,3}}, {<0,{}>, <1,{0}>, <1,{1}>, <1,{2}>, <1,{3}>, <2,{0,1}>, <2,{0,2}>, <2,{0,3}>, <2,{1,2}>, <2,{1,3}>, <2,{2,3}>, <3,{0,1,2}>, <3,{0,1,3}>, <3,{0,2,3}>, <3,{1,2,3}>}>.

Y su representación gráfica:

Ejemplo 3:

R	0	1	2	3
0	1	1	1	1
1	1	1	1	1
2	1	1	1	1
3	1	1	1	1

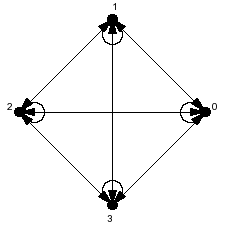
Cuyo dígrafo asociado sería:

G=<{0,1,2,3}, {<0, 0>, <0, 1>, <0, 2>, <0, 3>, <1, 0>, <1, 1>, <1, 2>, <1, 3>, <2, 0>, <2, 1>, <2, 2>, <2, 3>, <3, 0>, <3, 1>, <3, 2>, <3, 3>}>

para un posible aspector visual:

Ejemplo 4:

R	0	1	2	3
0	1	0	0	0
1	0	1	0	0
2	0	0	1	0
3	0	0	0	1

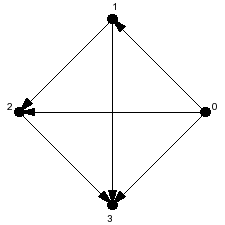
El dígrafo asociado:

G=<{0,1,2,3}, {<0, 0>, <1, 1>, <2, 2>, <3, 3>}>

para verse:

Ejemplo 5:

R	Sol	Tierra	Marte
Sol	0	0	0
Mercurio	1	0	0
Venus	1	0	0
Tierra	1	0	0
Luna	0	1	0
Marte	1	0	0
Fobos	0	0	1
Deimos	0	0	1

Cuyo dígrafo asociado se enuncia:

G=<{Sol, Mercurio, Venus, Tierra, Luna, Marte, Fobos, Deimos}, {<Mercurio, Sol>, <Venus, Sol>, <Tierra, Sol>, <Luna, Tierra>, <Marte, Sol>, <Fobos, Marte>, <Deimos, Marte>}>

que tiene el siguiente aspecto:

Propiedades

Las relaciones binarias se dividen en dos grandes grupos: las homogéneas y las heterogéneas, en dependencia de si los conjuntos A y B coinciden o no respectivamente; cada una con sus propiedades que permiten subclasificaciones.

Propiedades fundamentales de las relaciones binarias homogéneas.

Las relaciones binarias homogéneas hayan otras clasificaciones en tanto sus elementos satisfacen una serie de propiedades que veremos a continuación.

Relaciones reflexivas

Sea R una relación sobre A, se dice que es reflexiva si y solo si todo elemento de A está relacionado consigo mismo.

El caso más singular es el de las relaciones puramente reflexivas, también conocidas como identidades cuya formulación es I_A²={<x,x>| para toda x en A}.

Desde el punto de vista de la representación tabular esto se traduce en que toda la diagonal principal estará puesta a 1, como en los ejemplos 3 y 4 y en cuanto al grafo orientado asociado a la relación reflexiva, éste tiene lazos en todos sus nodos.

Relaciones irreflexivas

Una relación binaria homogénea R sobre el conjunto A es irreflexiva ssi no hay ni un solo par de la forma <x,x> en R.

Las matrices de las relaciones binarias irreflexivas tienen toda la diagonal principal puesta a 0, mientras que sus dígrafos nunca tienen lazos.

Los ejemplos 1, 2 y 5 son casos de relaciones irreflexivas.

Relaciones simétricas

La relación R sobre A es simétrica cuando para todo par <x,y> de R, su inverso <y,x> también pertenece a la relación.

Las relaciones simétricas tienen matrices simétricas respecto a la diagonal principal y sus dígrafos son fáciles de reconocer porque entre cualquier par de nodos diferentes hay o 2 o níngún arco. Pueden tener lazos.

Según lo antes visto son relaciones simétricas los casos de los ejemplos 3 y 4.

Relaciones antisimétricas

Toda relación binaria R sobre A es antisimétrica si se cumple que los pares <x,y> é <y,x> pertenecen a R si x=y.

Relaciones transitivas

Sea R una relación sobre A², ésta se dice transitiva si y solo si a R pertenecen los pares <x,y> e <y,z>, entonces <x,z> también.

Los ejemplos 3 y 4 son relaciones transitivas.

También lo es la versión "homogeneizada" de la relación del ejemplo 1.

Ejemplo 6: Sea A={0,1,2,3} y la relación binaria homogéneas R={<0,1>, <0,2>, <0,3>, <1,2>, <1,3>, <2,3>}

Su representaciones tabular sería:

R	1	2	3
0	1	1	1
1	0	1	1
2	0	0	1
3	0	0	0

Mientras que el grafo asociado:

Relaciones totales

Se dice que una relación binaria homogénea R sobre el conjunto A es total cuando entre cualquiera dos elementos distintos x,y de A xRy ó yRx.

Según la definición anterior solo el ejemplo 3 es total.

Otras clases de relaciones homogéneas

Existen otras clasificaciones de las relaciones homogéneas veamos por ejemplo:

Relaciones de dependencia: Son reflexivas y simétricas.
Preorden: Reflexiva y transitiva.
Orden parcial: Es un preorden antisimétrico.
Orden total: Es una relación orden parcial y a su vez es una relación total.
Relaciones de equivalencia: Reflexivas, simétricas y transitivas.

Relaciones y funciones

Las funciones son relaciones con particularidades bien definidas. La principal de ellas, que de hecho es la que la distingue es que un mismo elemento del dominio no puede tener dos imágenes distintas, cosa que sí es permisible en las relaciones.

Para los casos vistos en los ejemplos anteriores podemos identificar como funciones a los ejemplos 4 y 5. Los demás incumplen la definición de función.

Fuentes

García, Luciano. Lógica Matemática. Ediciones Revolucionarias. La Habana, 1988. Capítulo 2.
Artículo Relación binaria. Disponible en "es.wikipedia.org". Consultado: 8 de septiembre del 2011.

@@ Línea 5: / Línea 5: @@
 |concepto= Sean ''A'' y ''B'' conjuntos no vacíos, se llama '''relación binaria''' a cualquier subconjunto del producto cartesiano ''AxB''.
 }}
-<div align="justify">
 '''Relación binaria'''. Dícese en [[Matemática Discreta]] y [[Lógica]] de toda [[relación]] ''R'' que se establece entre los elementos de dos conjuntos no vacíos ''A'' y ''B'' y que se define mediante un [[conjunto]] de [[Par (Lógica)|pares]] ''<x,y>'', válidos para la propia relación con [[Archivo:x_en_A.gif|middle]] e [[Archivo:y_en_B.gif|middle]] y que indica.
-==Definición.==
+==Definición==
 Una relación binara ''R'' sobre ''A'' y ''B'', conjuntos no vacíos, indicada como ''R<sub>A,B</Sub>'', es un subconjunto de ''AxB''. Formalmente hablando sería [[Archivo:R_sub_A_B_subconjunto_A_x_B.gif|middle]]. Entonces, ''R<sub>A,B</sub>'' es un conjunto de pares ''<x,y>'' con [[Archivo:x_en_A.gif|middle]] e [[Archivo:y_en_B.gif|middle]].
@@ Línea 17: / Línea 16: @@
 Las siguientes notaciones son válidas ''xRy'', ''R(x,y)'', [[Archivo:X_y_en_R.gif|middle]], ''Rxy''([[notación polaca]]) y se leen '' '''x''' relacionado con '''y''' según '''R'''. ''
-==Ejemplos.==
+==Ejemplos==
 # ''A={0, 1, 2, 3}'', ''B={0, 1, 2, 3, 4, 5}'', ''R<sub>A,B</sub>={<0,1>, <0,2>, <0,3>, <0,4>, <0,5>, <1,2>, <1,3>, <1,4>, <1,5>, <2,3>, <2,4>, <2,5>, <3,4>, <3,5>}''.
 # ''A={0, 1, 2, 3}'', [[Archivo:B_igual_rho_A.gif|middle]], ''R<sub>A,B</sub>={<0,{}>, <1,{0}>, <1,{1}>, <1,{2}>, <1,{3}>, <2,{0,1}>, <2,{0,2}>, <2,{0,3}>, <3,{0,1,2}>, <3,{0,1,3}>,  <3,{0,2,3}>, <3,{1,2,3}>}''.
 # ''A={0,1,2,3}'', ''R<sub>A<sup>2</sup></sub>=A<sup>2</sup>={<0, 0>, <0, 1>, <0, 2>, <0, 3>, <1, 0>, <1, 1>, <1, 2>, <1, 3>, <2, 0>, <2, 1>, <2, 2>, <2, 3>, <3, 0>, <3, 1>, <3, 2>, <3, 3>}''.
 # ''A={0,1,2,3}'', ''R<sub>A<sup>2</sup></sub>=A<sup>2</sup>={<0, 0>, <1, 1>, <2, 2>, <3, 3>}''.
-# Sea ''C'' los siguientes cuerpos del [[Sistema Solar Interior]]: ''C={[[Sol]], [[Mercurio]], [[Venus]], [[Tierra]], [[Luna]], [[Marte]], [[Fobos]], [[Deimos]]}'', se define la relación ''' ''x'' gira alrededor de ''y'' ''' como ''G={<Mercurio, Sol>, <Venus, Sol>, <Tierra, Sol>, <Luna, Tierra>, <Marte, Sol>, <Fobos, Marte>, <Deimos, Marte>}''.
+# Sea ''C'' los siguientes cuerpos del [[Sistema Solar Interior]]: ''C={[[Sol]], [[Mercurio]], [[Venus]], [[Tierra]], [[Luna]], [[Marte]], [[Fobos]], [[Deimos (satélite)|Deimos]]}'', se define la relación ''' ''x'' gira alrededor de ''y'' ''' como ''G={<Mercurio, Sol>, <Venus, Sol>, <Tierra, Sol>, <Luna, Tierra>, <Marte, Sol>, <Fobos, Marte>, <Deimos, Marte>}''.
-==Representación.==
+==Representación==
 Las relaciones binarias pueden representarse de manera explícita como vimos en los ejemplos anteriores o de forma implícita en tanto también son conjuntos. No obstante existen otras formas de representarlas que ayudan a visualizar de modo más fácil algunas propiedades que pueden caracterorarlas. Entre las más notables están la representación tabular y la del dígrafo asociado, por lo que en el último caso puede llegar a obtenerse un esquema gráfico de las relaciones.
-===Representación tabular.===
+===Representación tabular===
 La representación tabular o [[Matriz|matricial]] de las relaciones binarias es simple y sigue la siguiente estructura.
@@ Línea 38: / Línea 37: @@
 *Para cada celda de la fila ''i'', columna ''j'': si ''iRj'', se indica 1; de lo contrario, 0.
-===Dígrafo asociado.===
+===Dígrafo asociado===
 Sea ''R'' una relación binaria sobre ''A'' y ''B'', se entiende por '''dígrafo asociado a ''R'' ''', al [[dígrafo|grafo orientado]] ''G=<A U B, R>''; es decir, cuyos vértices serán los elementos de A y B y sus arcos, los pares pertenecientes a la relación en cuestión.
-===Ejemplos.===
+===Ejemplos===
 Para el ejemplo 1, su representación tabular es:
@@ Línea 200: / Línea 199: @@
 * [[Archivo:Digrafo_asociado_ejemplo5.png|middle]]
-==Propiedades.==
+==Propiedades==
 Las relaciones binarias se dividen en dos grandes grupos: las homogéneas y las heterogéneas, en dependencia de si los conjuntos ''A'' y ''B'' coinciden o no respectivamente; cada una con sus propiedades que permiten subclasificaciones.
@@ Línea 206: / Línea 205: @@
 Las relaciones binarias homogéneas hayan otras clasificaciones en tanto sus elementos satisfacen una serie de propiedades que veremos a continuación.
-====Relaciones reflexivas.====
+====Relaciones reflexivas====
 Sea ''R'' una relación sobre ''A'', se dice que es '''reflexiva''' si y solo si todo elemento de ''A'' está relacionado consigo mismo.
@@ Línea 213: / Línea 212: @@
 Desde el punto de vista de la representación tabular esto se traduce en que <u>toda</u> la diagonal principal estará puesta a 1, como en los ejemplos 3 y 4 y en cuanto al grafo orientado asociado a la relación reflexiva, éste tiene lazos en <u>todos</u> sus nodos.
-====Relaciones irreflexivas.====
+====Relaciones irreflexivas====
 Una relación binaria homogénea ''R'' sobre el conjunto ''A'' es '''irreflexiva''' ssi no hay ni un solo par de la forma ''<x,x>'' en ''R''.
@@ Línea 220: / Línea 219: @@
 Los ejemplos 1, 2 y 5 son casos de relaciones irreflexivas.
-====Relaciones simétricas.====
+====Relaciones simétricas====
 La relación ''R'' sobre ''A'' es ''simétrica'' cuando para todo par ''<x,y>'' de ''R'', su inverso ''<y,x>'' también pertenece a la relación.
@@ Línea 227: / Línea 226: @@
 Según lo antes visto son relaciones simétricas los casos de los ejemplos 3 y 4.
-====Relaciones antisimétricas.====
+====Relaciones antisimétricas====
 Toda relación binaria ''R'' sobre ''A'' es '''antisimétrica''' si se cumple que los pares ''<x,y>'' é ''<y,x>'' pertenecen a ''R'' si ''x=y''.
-====Relaciones transitivas.====
+====Relaciones transitivas====
 Sea ''R'' una relación sobre ''A<sup>2</sup>'', ésta se dice '''transitiva''' si y solo si a ''R'' pertenecen los pares ''<x,y>'' e ''<y,z>'', entonces ''<x,z>'' también.
@@ Línea 261: / Línea 260: @@
 * [[Archivo:Digrafo_asociado_ejemplo6.png|middle]]
-====Relaciones totales.====
+====Relaciones totales====
-Se dice que una relación binaria homogénea es '''total''' cuando el grafo asociado es conexo.
+Se dice que una relación binaria homogénea ''R'' sobre el conjunto ''A'' es '''total''' cuando entre cualquiera dos elementos distintos ''x,y'' de ''A'' ''xRy'' ó ''yRx''.
 Según la definición anterior solo el ejemplo 3 es total.
-====Relaciones de equivalencia.====
+====Otras clases de relaciones homogéneas====
-Un relación binaria homogénea se dice que es de '''equivalencia''' ssi es reflexiva, simétrica y transitiva
-====Otras clases de relaciones homogéneas.====
 Existen otras clasificaciones de las relaciones homogéneas veamos por ejemplo:
-* '''Relaciones de dependencia''': Reflexiva y simétrica.
+* '''Relaciones de dependencia''': Son reflexivas y simétricas.
 * '''Preorden''': Reflexiva y transitiva.
 * '''Orden parcial''': Es un preorden antisimétrico.
 * '''Orden total''': Es una relación orden parcial y a su vez es una relación total.
+* '''Relaciones de equivalencia''': Reflexivas, simétricas y transitivas.
-==Relaciones y funciones.==
+==Relaciones y funciones==
 Las funciones son relaciones con particularidades bien definidas. La principal de ellas, que de hecho es la que la distingue es que un mismo elemento del dominio no puede tener dos imágenes distintas, cosa que sí es permisible en las relaciones.
 Para los casos vistos en los ejemplos anteriores podemos identificar como funciones a los ejemplos 4 y 5. Los demás incumplen la definición de función.
-==Veáse también.==
+==Fuentes==
-* [[Relación matemática]].
-* [[Relación n aria]].
-==Fuentes.==
 # [[Luciano García|García, Luciano]]. Lógica Matemática. Ediciones Revolucionarias. [[La Habana]], [[1988]]. Capítulo 2.
-# [http://es.wikipedia.org/wiki/Relación_binaria Relación binaria en [[Wikipedia]]].
+# Artículo [http://es.wikipedia.org/wiki/Relación_binaria Relación binaria]. Disponible en "es.wikipedia.org". Consultado: 8 de septiembre del 2011.
-</div>
 [[Categoría:Álgebra]]

Anónimo

Buscar

Navegación

Navegación

Solicitudes

Herramientas wiki

Herramientas wiki

Diferencia entre revisiones de «Relación binaria»

Espacios de nombres

Acciones de página

última versión al 15:14 2 oct 2020

Sumario

Definición

Ejemplos