¿No sabes por dónde empezar? Ayúdanos normalizando artículos.
¿Tienes experiencia? Crea alguno de estos artículos de actualidad.
Diferencia entre revisiones de «Desplazamiento angular»
(→Unidad de Medida) |
|||
| Línea 6: | Línea 6: | ||
}} | }} | ||
''' Desplazamiento Angular '''. Se refiere a la trayectoria en forma de [[ángulo]] que despliega un cuerpo durante el movimiento de giro, de igual forma se puede decir que el [[desplazamiento]] angular es igual a la diferencia entre la posición angular final y la posición angular inicial. El símbolo del desplazamiento angular es Δθ, donde la letra griega [[delta]] (Δ) denota el incremento de una [[magnitud]] y la letra griega theta (θ) se utiliza para la posición angular. Por tanto, el símbolo del desplazamiento angular, Δθ, significa el incremento de posición angular. | ''' Desplazamiento Angular '''. Se refiere a la trayectoria en forma de [[ángulo]] que despliega un cuerpo durante el movimiento de giro, de igual forma se puede decir que el [[desplazamiento]] angular es igual a la diferencia entre la posición angular final y la posición angular inicial. El símbolo del desplazamiento angular es Δθ, donde la letra griega [[delta]] (Δ) denota el incremento de una [[magnitud]] y la letra griega theta (θ) se utiliza para la posición angular. Por tanto, el símbolo del desplazamiento angular, Δθ, significa el incremento de posición angular. | ||
| + | |||
==Unidad de Medida== | ==Unidad de Medida== | ||
| − | Comúnmente la unidad con la que se expresa el [[desplazamiento]] angular es el [[radián]], ocasionalmente pueden utilizarse otras unidades de medida angulares como los grados o las revoluciones (2π radianes es equivalente a 360º) | + | |
| + | Comúnmente la unidad con la que se expresa el [[desplazamiento]] angular es el [[radián]], ocasionalmente pueden utilizarse otras unidades de medida angulares como los grados o las revoluciones (2π radianes es equivalente a 360º). | ||
==Fórmula== | ==Fórmula== | ||
| + | |||
Para calcular el [[desplazamiento]] angular de un cuerpo se debe restar su posición angular final menos su posición angular inicial. | Para calcular el [[desplazamiento]] angular de un cuerpo se debe restar su posición angular final menos su posición angular inicial. | ||
| + | |||
Δd = θ f – θ i | Δd = θ f – θ i | ||
| + | |||
Donde: | Donde: | ||
| + | |||
Δd es el desplazamiento angular | Δd es el desplazamiento angular | ||
| + | |||
θ f es la posición angular final | θ f es la posición angular final | ||
| + | |||
θ I es la posición angular inicial | θ I es la posición angular inicial | ||
| + | |||
==Velocidad== | ==Velocidad== | ||
| + | |||
La [[velocidad angular]] es la velocidad a la que el cuerpo recorre el desplazamiento angular, por tanto la [[velocidad angular]] es equivalente a la diferencia entre la posición angular final y la posición angular inicial partido por la diferencia entre el instante de [[tiempo]] final y el instante de [[tiempo]] inicial. | La [[velocidad angular]] es la velocidad a la que el cuerpo recorre el desplazamiento angular, por tanto la [[velocidad angular]] es equivalente a la diferencia entre la posición angular final y la posición angular inicial partido por la diferencia entre el instante de [[tiempo]] final y el instante de [[tiempo]] inicial. | ||
| + | |||
ω=Δθ/Δt | ω=Δθ/Δt | ||
| − | Donde | + | Donde: |
| + | |||
ω representa la [[frecuencia]] cíclica del cuerpo. | ω representa la [[frecuencia]] cíclica del cuerpo. | ||
| + | |||
Δθ se define como la variación que posee el [[ángulo]] durante su trayectoria sobre el [[espacio]]. | Δθ se define como la variación que posee el [[ángulo]] durante su trayectoria sobre el [[espacio]]. | ||
| + | |||
Δt es el intervalo de [[tiempo]], es decir, el [[tiempo]] que le toma al objeto recorrer un [[vector]] desde un punto "A" hacia un punto "B" en forma circular. | Δt es el intervalo de [[tiempo]], es decir, el [[tiempo]] que le toma al objeto recorrer un [[vector]] desde un punto "A" hacia un punto "B" en forma circular. | ||
| + | |||
==Importancia== | ==Importancia== | ||
| + | |||
El desplazamiento angular tiene diversas aplicaciones en la vida cotidiana y en la [[ciencia]]. Por ejemplo, se utiliza para estudiar la [[aceleración centrípeta]], la [[fuerza centrípeta]], la [[velocidad angular]], la [[energía cinética]] y la [[energía potencial]]. | El desplazamiento angular tiene diversas aplicaciones en la vida cotidiana y en la [[ciencia]]. Por ejemplo, se utiliza para estudiar la [[aceleración centrípeta]], la [[fuerza centrípeta]], la [[velocidad angular]], la [[energía cinética]] y la [[energía potencial]]. | ||
| + | |||
==Fuente== | ==Fuente== | ||
| + | |||
*Mingot,Tomás de Galiana. Pequeño Larousse de Ciencias y Técnicas. Pág.361 | *Mingot,Tomás de Galiana. Pequeño Larousse de Ciencias y Técnicas. Pág.361 | ||
*https://www.ingenierizando.com/cinematica/desplazamiento-angular/ | *https://www.ingenierizando.com/cinematica/desplazamiento-angular/ | ||
| + | |||
[[Category:Física]] | [[Category:Física]] | ||
Revisión del 12:42 31 oct 2023
| ||||
Desplazamiento Angular . Se refiere a la trayectoria en forma de ángulo que despliega un cuerpo durante el movimiento de giro, de igual forma se puede decir que el desplazamiento angular es igual a la diferencia entre la posición angular final y la posición angular inicial. El símbolo del desplazamiento angular es Δθ, donde la letra griega delta (Δ) denota el incremento de una magnitud y la letra griega theta (θ) se utiliza para la posición angular. Por tanto, el símbolo del desplazamiento angular, Δθ, significa el incremento de posición angular.
Unidad de Medida
Comúnmente la unidad con la que se expresa el desplazamiento angular es el radián, ocasionalmente pueden utilizarse otras unidades de medida angulares como los grados o las revoluciones (2π radianes es equivalente a 360º).
Fórmula
Para calcular el desplazamiento angular de un cuerpo se debe restar su posición angular final menos su posición angular inicial.
Δd = θ f – θ i
Donde:
Δd es el desplazamiento angular
θ f es la posición angular final
θ I es la posición angular inicial
Velocidad
La velocidad angular es la velocidad a la que el cuerpo recorre el desplazamiento angular, por tanto la velocidad angular es equivalente a la diferencia entre la posición angular final y la posición angular inicial partido por la diferencia entre el instante de tiempo final y el instante de tiempo inicial.
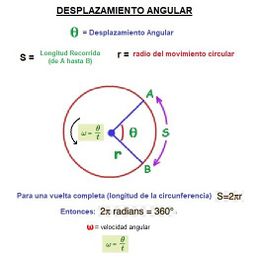
ω=Δθ/Δt Donde:
ω representa la frecuencia cíclica del cuerpo.
Δθ se define como la variación que posee el ángulo durante su trayectoria sobre el espacio.
Δt es el intervalo de tiempo, es decir, el tiempo que le toma al objeto recorrer un vector desde un punto "A" hacia un punto "B" en forma circular.
Importancia
El desplazamiento angular tiene diversas aplicaciones en la vida cotidiana y en la ciencia. Por ejemplo, se utiliza para estudiar la aceleración centrípeta, la fuerza centrípeta, la velocidad angular, la energía cinética y la energía potencial.
Fuente
- Mingot,Tomás de Galiana. Pequeño Larousse de Ciencias y Técnicas. Pág.361
- https://www.ingenierizando.com/cinematica/desplazamiento-angular/