Triángulo

Triángulo Concepto: Es la porción de plano limitada por una línea poligonal cerrada de tres lados, o sea, la parte de superficie plana limitada por tres segmentos.

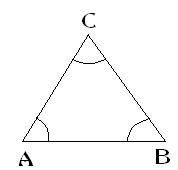
Triángulo(figura): Polígono de tres lados.

La suma de los tres ángulos de un triángulo es 180º. Dos de los ángulos son, necesariamente, agudos. El tercero puede ser también agudo, o bien recto u obtuso.

Definición.

Un triángulo es un polígono de 3 lados, siendo el menor de los polígonos en cuanto a la cantidad de lados. Las longitudes de todos los lados deben satisfacer la llamada Desigualdad triangular.

Clasificación.

Los triángulos se clasifican según la longitud de sus lados o según la amplitud de sus ángulos.

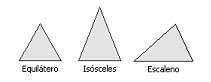
Según sus lados.

Según la longitud de sus lados, los triángulos se clasifican en:

• Triángulo equilátero: si sus tres lados son iguales.
• Triángulo isósceles: si tienen dos lados iguales.
• Triángulo escaleno: si los tres lados son distintos.

Clasificación según lados

Según sus ángulos.

La clasificación según angulos define las siguentes categorías:

• Triángulo acutángulo: Si todos los ángulos del triángulo son agudos.
• Triángulo rectángulo: Si tiene un ángulo recto. Estos triángulos también se denominan rectos.
• Triángulo obtusángulo: Estos triángulos poseen un ángulo obtuso.

Clasificación según ángulos

Alturas de un Triángulo

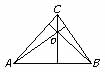
Se llama base de un triángulo a cualquiera de sus lados. El segmento perpendicular desde un vértice a la base opuesta o a su prolongación se llama altura. Un triángulo tiene, pues, tres bases a, b, c, y las tres alturas correspondientes, h_a, h_b y h_c.
En un triángulo rectángulo el cuadrado de la altura sobre la hipotenusa es igual al producto de los dos segmentos en que la divide: h² = m • n
Esta relación se conoce como teorema de la altura.
Las tres alturas de un triángulo (o sus prolongaciones) se cortan en un punto llamado ortocentro. Si el triángulo es acutángulo, el ortocentro es interior al triángulo.

Alturas del triángulo acutángulo

En un triángulo rectángulo, cada cateto puede ser considerado como base y como altura. El ortocentro es, por tanto, el vértice del ángulo recto. Si el triángulo es obtusángulo el ortocentro se obtiene, prolongando las alturas, fuera del triángulo.

Alturas del triángulo obtusángulo

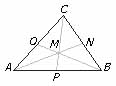
Medianas

Se llama mediana de un triángulo a cada uno de los tres segmentos que unen un vértice con el punto medio del lado opuesto. Las tres medianas de un triángulo se cortan en un punto que se llama baricentro.

Medianas de un triángulo

El baricentro corta a cada mediana en dos segmentos, uno de ellos la mitad del otro:

Proporciones que se cumplen

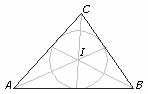
Circunferencia inscrita

Las bisectrices de los tres ángulos de un triángulo se cortan en un punto que se llama incentro porque es el centro de la circunferencia inscrita que es tangente a los tres lados del triángulo. Ésta es la mayor circunferencia contenida en el triángulo.

Circunferencia inscrita

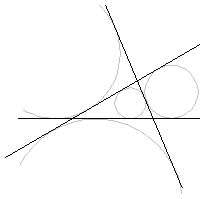
Circunferencia exinscritas

La bisectriz interior de un ángulo se corta con las dos bisectrices exteriores de los otros dos ángulos en un punto llamado exincentro, y que es centro de una circunferencia (exinscrita) tangente a un lado y a la prolongación de los otros dos.
Un triángulo tiene, pues, tres circunferencias exinscritas.

circunferencia exinscrita

Circunferencia circunscrita

Las mediatrices de los lados de un triángulo se cortan en un punto llamado circuncentro porque es centro de la circunferencia circunscrita que pasa por los tres vértices del triángulo. Esta es la menor circunferencia que contiene al triángulo.

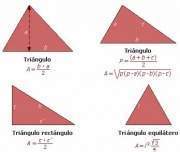
Área de un Triángulo

Triángulo medianas división.jpg

El Área de un triángulo de lados a, b, c, y alturas correspondientes h_a, h_b y h_c es: A = (1/2)a • ha = (1/2)b • hb = (1/2)c • hc
Si se conocen las longitudes de los tres lados, a, b, c, el área se puede calcular mediante la siguiente fórmula, llamada fórmula de Herón:

Triángulo área herón.jpg

en donde p = (a + b + c)/2 es el semiperímetro del triángulo.

Fuentes

• Microsoft ® Encarta ® 2007. © 1993--2006 Microsoft Corporation. Reservados todos los derechos.
• Miyares Arturo y Escalona Jose M. Geometría, Segundo Curso. Quinta Edición. Editorial Pueblo y Educación. La Habana. Cuba. 1974.