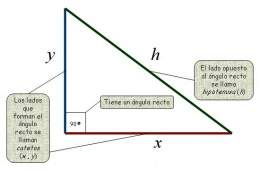
Triángulo rectángulo

Triángulo rectángulo Concepto: Triángulo con uno de sus ángulos interiores recto.

Triángulo rectángulo ó triángulo recto. Triángulo con un ángulo recto o de 90°.

Ángulos y lados en un triángulo recto.

Los ángulos interiores de un triángulo suman una amplitud de 180 grados.

En el caso de los triángulos rectos que poseen un ángulo de 90°, los otros dos ángulos interiores suman también 90° por lo que son ángulo(s) complementario(s).

En estos triángulos al lado opuesto al ángulo recto se le denomina hipotenusa, a otros dos lados adyacentes se les llama catetos.

Propiedades y cálculos.

El área de un triángulo rectángulo es igual a la mitad del producto de sus catetos (los catetos son perpendiculares por lo que pueden ser considerados base y altura del triángulo indistintamente).

Los triángulos rectángulos son la base del cáculo pitagórico y de la trigonometría circular.

En el primero de los casos existen las siguientes leyes que rigen el cáculo de los distintos elementos geométricos del triángulo.

• Teorema de las alturas.
• Teorema de los catetos.
• Teorema de Pitágoras.

Teorema del cateto.

El cuadrado de cada cateto es igual al producto de la hipotenusa por su proyección sobre ella, es decir:

• c² = a • m
• b² = a • n

Triángulo rectángulo

Teorema de Pitágoras.

El teorema de Pitágoras o de las hipotenusas plantea que el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.

Según la figura 1 quedaría:

• c² = a² + b²

Trigonometría.

Ademas de las relaciones que se establecen entre lados y alturas, también aparecen entre los lados y ángulos.

• Seno: Se define el seno de un ángulo como el cociente entre el lado opuesto al ángulo y la hipotenusa.
• Coseno: Se define el coseno de un ángulo como el cociente del lado adyacente al ángulo por la hipotenusa.
• Tangente: Se conoce por tangente de un ángulo la división del lado opuesto por el lado adyacente.
• Cotangente: Se conoce por cotangente de un ángulo la división del lado adyacente por el lado opuesto.

Reconocimiento de un triángulo rectángulo

• Midiendo con un transportador, el mayor ángulo medirá 90*
• Se forma un ángulo recto con un papel, doblando este y volviendo a superponer la primera doblez sobre sí misma y se tiene un "ángulo recto".
• Se circunscribe una circunferencia al triángulo ACB, de centro el punto medio del lado mayor AB, radio la mitad de este lado, si el ángulo opuesto C está en la circunferencia, el triángulo es rectángulo.
• Sea un triángulo ACB, c lado mayor. Si la suma (a/c)² + (b/c)² es 1, ACB es un triángulo rectángulo.
• Por el teorema de Babilonia- Pitágoras. c² = a² + b² , c lado mayor.

Fuentes

• ditutor.com