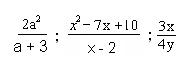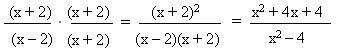Diferencia entre revisiones de «Fracción algebraica»
| Línea 23: | Línea 23: | ||
[[Image: Simplificación 1]] | [[Image: Simplificación 1]] | ||
Para amplificar una fracción algebraica se multiplica el numerador y el denominador de la fracción por un polinomio. | Para amplificar una fracción algebraica se multiplica el numerador y el denominador de la fracción por un polinomio. | ||
| − | Ejemplo | + | Ejemplo: |
| − | + | [[Image:Ampliación.JPG]] | |
| + | Para simplificar esta expresión algebraica dividimos el numerador y el denominador por 2m2n (que es el mayor factor común a ambos). | ||
| + | Ejemplo: | ||
| + | Simplifica las fracciones algebraicas siguientes: | ||
| + | [[Image:Ej 1 a).JPG]] | ||
| + | [[Image: Resuelto a).JPG]] | ||
| + | b) | ||
| + | [[Image:Imagen: Ej 1 b).JPG]] | ||
| + | Aquí no se puede simplificar directamente; tenemos que descomponer en factores el numerador y el denominador | ||
| + | [[Image: Resuelto b).JPG]] | ||
| + | c) | ||
| + | [[Image:Ej 1 c).JPG]] | ||
| + | Factorizando ambos trinomios: | ||
| + | [[Image: Resuelto c).JPG]] | ||
| + | ==Operaciones con fracciones== | ||
| + | ===Multiplicación=== | ||
| + | Para multiplicar fracciones algebraicas se procede de forma análoga que para multiplicar [[Fracciones|fracciones]] comunes. | ||
| + | Si tenemos las fracciones algebraicas se cumple que. | ||
| + | [[Image: Multiplicación.JPG]] | ||
| + | Con el objetivo de obtener un resultado ya simplificado, es conveniente proceder de la forma siguiente: | ||
| + | Factorizar los numeradores y denominadores de las fracciones dadas (cuando no lo estén ya). | ||
| + | Simplificar los factores que se comunes a los numeradores y denominadores. | ||
| + | Efectuar las multiplicaciones indicadas. | ||
| + | Ejemplo: | ||
| + | Efectúa las multiplicaciones siguientes: | ||
| + | a) | ||
| + | [[Image: Multiplic a).JPG]] | ||
| + | Como los denominadores y los numeradores son monomios, se procede a simplificar y después efectuamos los productos indicados. | ||
| + | [[Image: Resuelto Multiplic a).JPG]] | ||
| + | b) | ||
| + | [[Image: Multiplic b).JPG]] | ||
| + | Descomponemos en este caso el numerador del primer factor (diferencia de cuadrado), el numerador del segundo factor (binomio, extracción de factor común) y el denominador del segundo factor (trinomio) | ||
| + | Simplificamos y efectuamos la multiplicación | ||
| + | Eliminamos el paréntesis multiplicando 2 por m+2 | ||
| + | [[Image: Resuelto Multiplic b).JPG]] | ||
== Véase también. == | == Véase también. == | ||
*[[Expresiones Algebraicas|Expresiones Algebraicas]] | *[[Expresiones Algebraicas|Expresiones Algebraicas]] | ||
| − | |||
== Fuente == | == Fuente == | ||
Revisión del 17:34 25 may 2011
| ||||||
Fracción algebraica. Es el cociente de dos polinomios.
Sumario
Fracciones algebraicas
Si A y B son dos expresiones algebraicas con B ≠ 0, y en B aparece al menos una variable con exponente entero positivo, el cociente indicado recibe el nombre de fracción algebraica.
Fracciones algebraicas
Si A y B son dos expresiones algebraicas con B ≠ 0, y en B aparece al menos una variable con exponente entero positivo, el cociente indicado recibe el nombre de fracción algebraica.
Por ejemplo:
Simplificación y ampliación de fracciones algebraicas
En una fracción algebraica, al igual que una fracción numérica, también es posible multiplicar o dividir el numerador y el denominador por un mismo factor (diferente de cero), obteniéndose así una nueva fracción equivalente a la fracción dada.
Archivo:Simplificación 1 Para amplificar una fracción algebraica se multiplica el numerador y el denominador de la fracción por un polinomio. Ejemplo:
Para simplificar esta expresión algebraica dividimos el numerador y el denominador por 2m2n (que es el mayor factor común a ambos).
Ejemplo:
Simplifica las fracciones algebraicas siguientes:
.JPG)
Archivo:Resuelto a).JPG
b)
Archivo:Imagen: Ej 1 b).JPG
Aquí no se puede simplificar directamente; tenemos que descomponer en factores el numerador y el denominador
Archivo:Resuelto b).JPG
c)
.JPG)
Factorizando ambos trinomios:
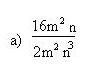
Archivo:Resuelto c).JPG
Operaciones con fracciones
Multiplicación
Para multiplicar fracciones algebraicas se procede de forma análoga que para multiplicar fracciones comunes.
Si tenemos las fracciones algebraicas se cumple que.
Con el objetivo de obtener un resultado ya simplificado, es conveniente proceder de la forma siguiente:
Factorizar los numeradores y denominadores de las fracciones dadas (cuando no lo estén ya).
Simplificar los factores que se comunes a los numeradores y denominadores.
Efectuar las multiplicaciones indicadas.
Ejemplo:
Efectúa las multiplicaciones siguientes:
a)
Archivo:Multiplic a).JPG
Como los denominadores y los numeradores son monomios, se procede a simplificar y después efectuamos los productos indicados.
Archivo:Resuelto Multiplic a).JPG
b)
.JPG)
Descomponemos en este caso el numerador del primer factor (diferencia de cuadrado), el numerador del segundo factor (binomio, extracción de factor común) y el denominador del segundo factor (trinomio) Simplificamos y efectuamos la multiplicación Eliminamos el paréntesis multiplicando 2 por m+2
.JPG)
Véase también.
Fuente
- Libro de texto de Matemática 9no Grado.
.JPG){kind=link}
.JPG){kind=link}
.JPG){kind=link}
.JPG){kind=link}
.JPG){kind=link}
.JPG){kind=link}