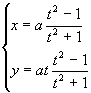Diferencia entre revisiones de «Estrofoide»
| Línea 10: | Línea 10: | ||
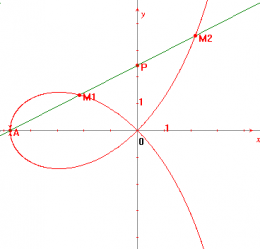
'''Estrofoide'''. Es el lugar geométrico de los puntos M1 y M2. (que yacen en rayos arbitrarios que pasan por el punto A), para los cuales PM1=PM2=OP (P es un punto arbitrario del eje Oy). | '''Estrofoide'''. Es el lugar geométrico de los puntos M1 y M2. (que yacen en rayos arbitrarios que pasan por el punto A), para los cuales PM1=PM2=OP (P es un punto arbitrario del eje Oy). | ||
| + | == Surgimiento == | ||
| + | |||
| + | Probablemente fue el científico francés [[Roberval]] ([[1602]] - [[1675]]) el primero que estudió esta curva, en [[1645]], y le dio el nombre de pteroide (pteron = ala). | ||
| + | |||
| + | El nombre estrofoide es debido a [[Montucci]] ([[1846]]) y viene del griego strofos que significa 'cordón, cuerda, lazo, correa'. | ||
== Definición == | == Definición == | ||
| + | Dado el sistema cartesiano ortonormal OXY sea A un punto sobre el eje x. Trazando por A una recta cualquiera AD que corte a OY en D, se lleva sobre esta recta, a un lado y otro de D los segmentos DM = DN = OD. El lugar geométrico de los puntos M y N se llama estrofoide. | ||
| + | |||
| + | [[Image:Estrofoide1.png|thumb|center|Estrofoide]] | ||
| + | |||
| + | == Ecuaciones == | ||
| + | Es el lugar geométrico de los puntos que satisfacen la [[ecuación implícita]]: | ||
| − | + | [[Image:EcuacEstrofoide.gif]] | |
| − | |||
La ecuación implícita anterior , tiene como [[ecuaciones paramétricas]] a: | La ecuación implícita anterior , tiene como [[ecuaciones paramétricas]] a: | ||
| + | |||
[[Image:EcuacParamEstrofoide.gif]] | [[Image:EcuacParamEstrofoide.gif]] | ||
| + | |||
donde el parámetro t es la tangente del triángulo BOx. | donde el parámetro t es la tangente del triángulo BOx. | ||
En coordenadas polares es: | En coordenadas polares es: | ||
| + | |||
[[Image:Coordpolares_estrofoide.gif]] | [[Image:Coordpolares_estrofoide.gif]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
== Fuentes == | == Fuentes == | ||
| − | * | + | *[http://perso.wanadoo.es/jpm/curvasfamosas/estrofoide.html Estrofoide] |
| − | *[http:// | + | *[http://prepa8.unam.mx/colegios/mate/geogebra/parametricas_i.html Ecuaciones Estrofoide] |
| − | + | *[http://personales.ya.com/jmreyes/curvas1.html Lugares geométricos] | |
| − | *[http:// | ||
[[Category:Matemáticas]][[Category:Geometría]] | [[Category:Matemáticas]][[Category:Geometría]] | ||
Revisión del 09:25 8 ago 2011
| ||||
Estrofoide. Es el lugar geométrico de los puntos M1 y M2. (que yacen en rayos arbitrarios que pasan por el punto A), para los cuales PM1=PM2=OP (P es un punto arbitrario del eje Oy).
Surgimiento
Probablemente fue el científico francés Roberval (1602 - 1675) el primero que estudió esta curva, en 1645, y le dio el nombre de pteroide (pteron = ala).
El nombre estrofoide es debido a Montucci (1846) y viene del griego strofos que significa 'cordón, cuerda, lazo, correa'.
Definición
Dado el sistema cartesiano ortonormal OXY sea A un punto sobre el eje x. Trazando por A una recta cualquiera AD que corte a OY en D, se lleva sobre esta recta, a un lado y otro de D los segmentos DM = DN = OD. El lugar geométrico de los puntos M y N se llama estrofoide.
Ecuaciones
Es el lugar geométrico de los puntos que satisfacen la ecuación implícita:
La ecuación implícita anterior , tiene como ecuaciones paramétricas a:
donde el parámetro t es la tangente del triángulo BOx.
En coordenadas polares es:
Archivo:Coordpolares estrofoide.gif