Diferencia entre revisiones de «Ley de Wien»
(Página creada con '<div align="justify"> {{Definición |nombre= Ley de Wien |imagen=Ley_de_Wien.gif |tamaño= |concepto= }}'''Ley de Wien.''' Formulada en 1893 por el físico alemán [[Wilhelm...') |
m (Texto reemplazado: «<div align="justify">» por «») |
||
| (No se muestran 6 ediciones intermedias de otro usuario) | |||
| Línea 1: | Línea 1: | ||
| − | + | ||
{{Definición | {{Definición | ||
|nombre= Ley de Wien | |nombre= Ley de Wien | ||
| − | |imagen=Ley_de_Wien. | + | |imagen=Ley_de_Wien.png |
|tamaño= | |tamaño= | ||
| − | |concepto= | + | |concepto=Para un cuerpo negro, el producto de la longitud de onda de máxima radiación y de la temperatura termodinámico es constante. Como resultado, cuando la temperatura sube, la máxima energía radiante cambia hacia longitudes de ondas más cortas ( energía y frecuencia más alta) y hacia el final del espectro. |
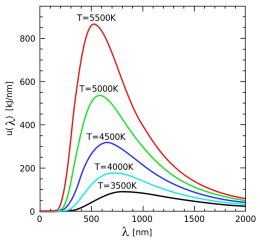
| − | }}'''Ley de Wien.''' Formulada en [[1893]] por el físico alemán [[Wilhelm Wien]], expresa de manera cuantitativa el hecho empírico mediante el cual el pico o máximo de emisión en el espectro de un cuerpo negro se desplaza hacia longitudes de onda más cortas (frecuencias mayores) a medida que aumenta la temperatura. | + | }}'''Ley de Wien.''' Formulada en [[1893]] por el físico alemán [[Wilhelm Wien]], expresa de manera cuantitativa el hecho empírico mediante el cual el pico o máximo de emisión en el espectro de un cuerpo negro se desplaza hacia longitudes de onda más cortas (frecuencias mayores) a medida que aumenta la [[temperatura]]. |
== Descripción == | == Descripción == | ||
| − | Cuando aumenta la temperatura de un radiador de [[cuerpo negro]], aumenta la energía radiada general, y el pico de la curva de radiación se mueve hacia longitudes de ondas más cortas. Cuando se evalúa el máximo a partir de la fórmula de radiación de Planck, se encuentra que el producto de la longitud de onda máxima y la temperatura es constante. | + | Cuando aumenta la temperatura de un radiador de [[cuerpo negro]], aumenta la energía radiada general, y el pico de la curva de radiación se mueve hacia longitudes de ondas más cortas. Cuando se evalúa el máximo a partir de la [[Ley de Planck|fórmula de radiación de Planck]], se encuentra que el producto de la longitud de onda máxima y la temperatura es constante. |
Esta relación se denomina ley del desplazamiento de Wien, y es útil para la determinación de la temperatura de objetos radiantes calientes tales como estrellas, y de hecho, para una determinación de la temperatura de cualquier objeto radiante, cuya temperatura es muy superior a la de su entorno. | Esta relación se denomina ley del desplazamiento de Wien, y es útil para la determinación de la temperatura de objetos radiantes calientes tales como estrellas, y de hecho, para una determinación de la temperatura de cualquier objeto radiante, cuya temperatura es muy superior a la de su entorno. | ||
| Línea 16: | Línea 16: | ||
La Ley de Wien es una ley de la física que especifica que hay una relación inversa entre la longitud de onda en la que se produce el pico de emisión de un cuerpo negro y su temperatura. | La Ley de Wien es una ley de la física que especifica que hay una relación inversa entre la longitud de onda en la que se produce el pico de emisión de un cuerpo negro y su temperatura. | ||
| + | [[Archivo:Formulación_de_la_Ley_de_Wien.JPG|center]] | ||
| + | donde T es la temperatura del cuerpo negro en Kelvin (K) y λ<sub>max</sub> es la longitud de onda del pico de emisión en metros. | ||
| + | Las consecuencias de la ley de Wien es que cuanta mayor sea la temperatura de un cuerpo negro menor es la longitud de onda en la cual emite. Por ejemplo, la temperatura de la fotosfera solar es de 5780 K y el pico de emisión se produce a 500 nanometros (5x10<sup>-7</sup> metros). Esta longitud de onda corresponde aproximadamente al centro del espectro visible siendo por lo tanto un tono de verde. | ||
| − | + | Sin embargo, debido a la [[difusión de Rayleigh]] de la luz azul por la [[atmósfera]] la componente azul se separa distribuyéndose por la bóveda celeste y el [[Sol]] aparece amarillento. | |
| − | |||
== Aplicaciones == | == Aplicaciones == | ||
| + | [[Archivo:Temperaturas_de_estrellas.gif|thumb|right|450px|Gráfico de temperaturas de estrellas según la Ley de Wien.]] | ||
| + | Una de las aplicaciones más importantes de la ley de Wien es la obtención de datos de sobre una estrella. Sabiendo que los picos de emisión de [[Radiación electromagnética|radiación electromagnética]] se tienen en una longitud de onda diferente según varíe la temperatura, es posible medir la cantidad de radiación que se emite por una estrella para conocer la temperatura a la cual se encuentra la superficie de la misma. | ||
| − | + | Habiendo determinado su temperatura es posible hacer estimaciones de la masa de estrellas lejanas, pues la energía que alimenta sus emisiones proviene de la fusión de [[Núcleo Atómico|núcleos de átomos]] (principalmente núcleos de [[hidrógeno]]) y esta fusión de núcleos es solo posible por la enorme gravedad de la estrella (que es consecuencia de la masa) que presiona partículas entre sí. | |
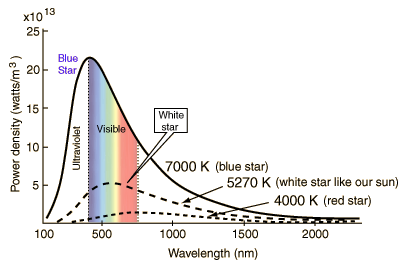
| − | + | Las estrellas se aproximan a radiadores de cuerpo negro, y sus colores visibles dependen de la temperatura del radiador. Las curvas muestran estrellas azules, blancas y rojas. La estrella blanca se ajusta a 5270K, de modo que el pico de su curva de cuerpo negro, está a la longitud de onda de pico del Sol, 550 nm. | |
== Fuentes == | == Fuentes == | ||
| − | *http://www.cida.ve/~briceno/cursos/astrof_observ/clase3/wien.html | + | *''Ley de Wien''. Disponible en: http://www.cida.ve/~briceno/cursos/astrof_observ/clase3/wien.html. Consultado el [[27 de diciembre]] de [[2013]]. |
| − | *http://hyperphysics.phy-astr.gsu.edu/hbasees/wien.html | + | *''Ley de Desplazamiento de Wien''. Disponible en: http://hyperphysics.phy-astr.gsu.edu/hbasees/wien.html. Consultado el 27 de diciembre de 2013. |
| − | *http://enciclopedia.us.es/index.php/Ley_de_Wien | + | *''Ley de Wien'', publicado el [[1 de diciembre]] de [[2004]]. Disponible en: http://enciclopedia.us.es/index.php/Ley_de_Wien. Consultado el 27 de febrero de 2013. |
| − | + | *''Definición de la Ley de Wien''. Disponible en: http://www.diclib.com/Ley%20de%20Wien/show/es/es_astronomia/L/75/0/0/1/565. Consultado el [[28 de febrero]] de [[2013]]. | |
| − | [[Categoría:Leyes]] | + | [[Categoría:Mecánica Cuántica]][[Categoría:Leyes]] |
última versión al 08:16 27 ago 2019
Ley de Wien. Formulada en 1893 por el físico alemán Wilhelm Wien, expresa de manera cuantitativa el hecho empírico mediante el cual el pico o máximo de emisión en el espectro de un cuerpo negro se desplaza hacia longitudes de onda más cortas (frecuencias mayores) a medida que aumenta la temperatura.
Descripción
Cuando aumenta la temperatura de un radiador de cuerpo negro, aumenta la energía radiada general, y el pico de la curva de radiación se mueve hacia longitudes de ondas más cortas. Cuando se evalúa el máximo a partir de la fórmula de radiación de Planck, se encuentra que el producto de la longitud de onda máxima y la temperatura es constante.
Esta relación se denomina ley del desplazamiento de Wien, y es útil para la determinación de la temperatura de objetos radiantes calientes tales como estrellas, y de hecho, para una determinación de la temperatura de cualquier objeto radiante, cuya temperatura es muy superior a la de su entorno.
Formulación
La Ley de Wien es una ley de la física que especifica que hay una relación inversa entre la longitud de onda en la que se produce el pico de emisión de un cuerpo negro y su temperatura.
donde T es la temperatura del cuerpo negro en Kelvin (K) y λmax es la longitud de onda del pico de emisión en metros. Las consecuencias de la ley de Wien es que cuanta mayor sea la temperatura de un cuerpo negro menor es la longitud de onda en la cual emite. Por ejemplo, la temperatura de la fotosfera solar es de 5780 K y el pico de emisión se produce a 500 nanometros (5x10-7 metros). Esta longitud de onda corresponde aproximadamente al centro del espectro visible siendo por lo tanto un tono de verde.
Sin embargo, debido a la difusión de Rayleigh de la luz azul por la atmósfera la componente azul se separa distribuyéndose por la bóveda celeste y el Sol aparece amarillento.
Aplicaciones
Una de las aplicaciones más importantes de la ley de Wien es la obtención de datos de sobre una estrella. Sabiendo que los picos de emisión de radiación electromagnética se tienen en una longitud de onda diferente según varíe la temperatura, es posible medir la cantidad de radiación que se emite por una estrella para conocer la temperatura a la cual se encuentra la superficie de la misma.
Habiendo determinado su temperatura es posible hacer estimaciones de la masa de estrellas lejanas, pues la energía que alimenta sus emisiones proviene de la fusión de núcleos de átomos (principalmente núcleos de hidrógeno) y esta fusión de núcleos es solo posible por la enorme gravedad de la estrella (que es consecuencia de la masa) que presiona partículas entre sí.
Las estrellas se aproximan a radiadores de cuerpo negro, y sus colores visibles dependen de la temperatura del radiador. Las curvas muestran estrellas azules, blancas y rojas. La estrella blanca se ajusta a 5270K, de modo que el pico de su curva de cuerpo negro, está a la longitud de onda de pico del Sol, 550 nm.
Fuentes
- Ley de Wien. Disponible en: http://www.cida.ve/~briceno/cursos/astrof_observ/clase3/wien.html. Consultado el 27 de diciembre de 2013.
- Ley de Desplazamiento de Wien. Disponible en: http://hyperphysics.phy-astr.gsu.edu/hbasees/wien.html. Consultado el 27 de diciembre de 2013.
- Ley de Wien, publicado el 1 de diciembre de 2004. Disponible en: http://enciclopedia.us.es/index.php/Ley_de_Wien. Consultado el 27 de febrero de 2013.
- Definición de la Ley de Wien. Disponible en: http://www.diclib.com/Ley%20de%20Wien/show/es/es_astronomia/L/75/0/0/1/565. Consultado el 28 de febrero de 2013.