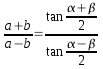Teorema de la tangente

Teorema de la tangente Concepto: Teorema de la geometría de triángulos que relaciona la suma y diferencia de dos lados con las tangentes de los ángulos correspondientes.

Teorema del coseno. En Geometría y más específicamente en Geometría euclidiana, se trata de un teorema de la trigonometría que en cada triángulo indica la relación entre la proporción de las suma y la diferencia de las longitudes de dos lados con las tangentes de la mitad de las amplitudes de la suma y la resta de los ángulos opuestos a dichos lados.

Definición.

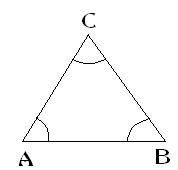
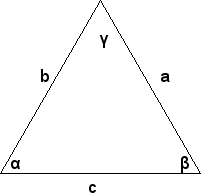
Sea un triángulo cualquiera como el de la figura:

• 

El teorema de las tangentes plantea que la suma de las longitudes de dos lados es a la diferencia de esos dos lados como la tangente de la mitad de la amplitud total de los ángulos opuestos a dichos lados es a la tangente de la mitad de la diferencia de dichos ángulos.

O lo que es lo mismo:

• 
• 
• 

Implicaciones e importancia.

El teorema de las tangentes juega un papel de gran relevancia en el cálculo y definición de superficies y volúmenes que pueden contener triángulos. Junto con la desigualdad triangular, el teorema de los senos y cosenos, permiten una caracterización de los elementos conformantes (las longitudes de los lados y amplitudes de los ángulos interiores de los triángulos), de manera que primero pueda distinguirse que estos conforman un triángulo y además, la relación de los mismos con sus ángulos, entre otras muchas propiedades.

Veáse también.

• Teorema del seno.
• Teorema del coseno.

Fuentes.

1. I. Bronshtein, K. Semendiaev. Manual de matemáticas para ingenieros y estudiantes. 2da Edición. Editorial MIR, Moscú. 1973.
2. Colectivo de autores. Matemática 10mo grado. Editorial Pueblo y Educación, La Habana. 1989.
3. Teorema de los senos en Wikipedia. Revisado 29 de marzo de 2012.