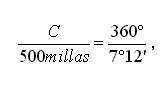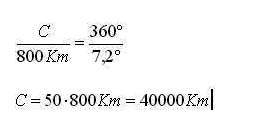Trigonometría
| ||||||
Trigonometría. Reúne en una sola teoría dos tipos diferentes de aplicaciones, para estudiar relaciones numéricas entre los lados y los ángulos de los triángulos y analizar los problemas relativos a los hechos periódicos.
Sumario
Antecedentes
Historia
La palabra Trigonometría es una combinación de dos palabras (del griego trigonom triángulo; metro media). Tuvo sus orígenes en Grecia y Egipto, su estudio tiene una historia continua, desde su origen hasta la actualidad. El nombre originalmente correcto, es inadecuado en la actualidad, puesto que la medición de triángulos no es la única aplicación importante para esta materia en la actualidad.
Para hallar sus orígenes nos trasladamos hasta el siglo II (ane), en sus comienzos estaba estrictamente relacionada con la Geometría, tiene su origen al parecer, con la aplicación de los principios geométricos a los problemas de deslizamiento de terrenos, así como a la astronomía. En este propio siglo, el matemático Hiparco (180-125 ane), nacido en Nicea, Asia Menor y considerado el más destacado de los astrónomos griegos, inicia el uso de una tabla de cuerdas de la circunferencia que en cierto modo equivalía a una tabla rudimentaria de valores del seno.
En su astronomía, Hiparco había introducido la división Sexagesimal de los Babilonios y otro matemático relevante, Claudio Ptolomeo (Tolomeo) (griego residente en Alejandría) solo unos años más tarde continúa el uso de esta división, y en su obra el “Almagesto”, calcula una tabla de cuerdas y llega a expresiones en las que si se cambia la palabra “cuerda” por “doble del seno del arco mitad” se obtendrían algunas fórmulas de la actual trigonometría.
Existen antecedentes aislados del uso de la trigonometría en época anteriores; ejemplo los egipcios habían utilizado los principios de la trigonometría para restablecer los linderos de la parcelas a lo largo del río Nilo, que se desaparecían a cauda de las crecientes del río todos los años.
El desarrollo de todos estos principios en una teoría coherente, para la solución de problemas más complicados se atribuye a Hiparco.
Este se consideró el más destacado Astrónomo de la antigua Grecia. Siendo muy adolescente al salir de su clase de Geometría se preguntaba como podía usar los conocimientos recibidos en relación con la amplitud y las propiedades de los ángulos.
Esta preocupación en él se resolvió años después al calcular la distancia entre la Tierra y alguno de los astros conocidos en ese tiempo.Mediante medios rudimentarios para medir la amplitud de un ángulo (astrolabio) pudo calcular con una precisión increíble para su época que la distancia máxima entre la Tierra y la Luna era de unos 400 000 Km.
Comparado con los cálculos actuales que estiman 385 000 Km ofrece solo un error de 3.5%
La trigonometría no solo permite calcular elementos de un triángulo, sino que es también posible resolver de forma sencilla, muchos problemas de la vida práctica cuya solución presentaría grandes dificultades por otros métodos o sería imposible
Curioso
Para los poco familiarizados con la historia clásica de Grecia se maravillarían al conocer el avance científico que ya tenían en esa época, por ejemplo, los griegos ya habían descubierto que la Tierra era esférica, usando la geometría y la trigonometría habían estimado su diámetro y el de la Luna con exactitud sorprendente. Estos descubrimientos quedaron olvidados por más de 1000 años siendo considerados nuevamente en tiempos de Cristóbal Colón.
Más cercano
En el siglo IX los árabes adoptaron y desarrollaron la Trigonometría Hindú y el astrónomo Al Battari usa, además del seno, la tangente, la cotangente y da un paso importante al aplicar el álgebra a la trigonometría. El primer texto árabe en el que aparece la trigonometría como una ciencia independiente se debe al astrónomo persa Nassir-eddin (1201-1274). Con la entrada de los árabes a Europa se difunden sus conocimientos matemáticos, se publica el primer tratado de trigonometría, escrito en latín en 1464, escrito por el matemático alemán J. Müller y en ella muestra de forma sencilla y elegante el teorema de los senos.
El importante desarrollo de Francois Vieta (1540-1603) logró con el álgebra simbólica aplicarla a la trigonometría y obtener por procedimientos algebraicos con todas las identidades fundamentales de la actual trigonometría.
Después de Tolomeo hubo pocas adiciones a la trigonometría, hasta el siglo XVII, momento en el cual ideas de muchos matemáticos han influido en el desarrollo de esta disciplina.
Aportes de la teoría
La trigonometría reúne en una sola teoría dos tipos diferentes de aplicaciones. Los métodos trigonométricos, pueden ser utilizados, para estudiar relaciones numéricas entre los lados y los ángulos de los triángulos y, por otro lado, analizar los problemas relativos a los hechos periódicos como veremos más adelante.
Ejemplo de aplicaciones tenemos que dentro del primer tipo se pueden ver deslindamiento de terrenos, astronomía, navegación, mecánica; en el segundo tipo se presentan en estudio de fenómenos eléctricos, Teoría de las vibraciones y en otras ramas de la ciencia e ingeniaría moderna.
Algo que se debe saber
Para comprender la teoría que se soporta en la trigonometría es necesario conocer algunos elementos básicos.
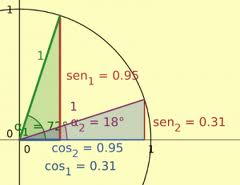
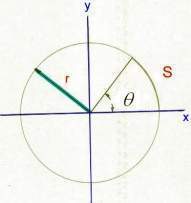
1. Circunferencia en un eje de coordenadas. Un círculo de radio positivo r con su centro en el origen de un sistema de coordenadas rectangulares m.
- Si el círculo se divide en 360 ángulos centrales iguales, cada uno es la unidad para la medida del sistema sexagesimal. Por tanto, a la circunferencia entera corresponde un arco de 360 grados (360˚). Un grado es igual a 60 minutos (60´) e igual a 3600 segundos (3600´´).
- La longitud de la circunferencia de radio r unidades es igual a 2πr unidades
- En un mismo círculo, los ángulos centrales son proporcionales a sus arcos correspondientes.
2. Razones trigonométricas Según el Teorema de Pitágoras existe relación entre los lados de un Triángulo rectángulo, también en este tipo de triángulo existe relación entre sus Ángulos, además de relaciones entre lados y ángulos que se expresan mediante razones trigonométricas, seno, coseno, tangente.
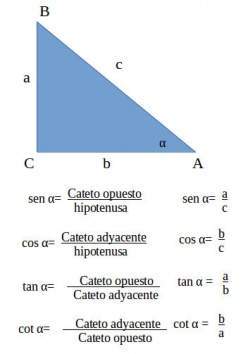
Definición: Sea α un ángulo agudo de vértice A de un triángulo rectángulo ABC. Sean a y b los catetos y c la hipotenusa, se llama:
- Seno de α y se denota sen α, a la razón a/c, entre el cateto opuesto a α y la hipotenusa.
- Coseno de α y se denota cos α, a la razón b/c , entre el cateto adyacente a α y la hipotenusa.
- Tangente de α y se denota tan α, a la razón a/b, entre el cateto opuesto y el adyacente a dicho ángulo.
- Cotangente de α y se denota tan α, a la razón b/a, entre el cateto adyacente y el opuesto a dicho ángulo.
Esquema para recordar:
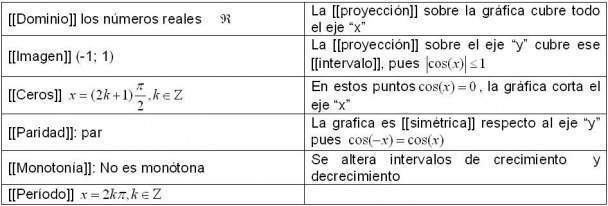
Función coseno
Poner propiedades y función
Aplicaciones
Trigonometría y hechos periódicos
En el mundo físico ocurren muchos hechos periódicos, la sucesión de los días y las noches, las fases de la luna, la aparición de los Cometas, el flujo y reflujo de la marea, y en menor escala, el movimiento del péndulo. La acción de los pistones de una máquina de combustión interna, la rotación de las manecillas del reloj. Todos estos hechos ocurren en forma periódica (o casi periódica). Uno de los propósitos de las matemáticas es suministrar un lenguaje simbólico y expresiones mediante el cual se puedan describir los hechos del mundo físico.
A partir del conocimiento de las propiedades de las funciones trigonométricas identificamos que las mismas son funciones periódicas, en ellas se manifiestan propiedades que nos ayudan a resolver problemas relacionados con la periodicidad y por tanto nos ayudan a solucionar problemas prácticos de la física.
Primera propiedad es el desplazamiento
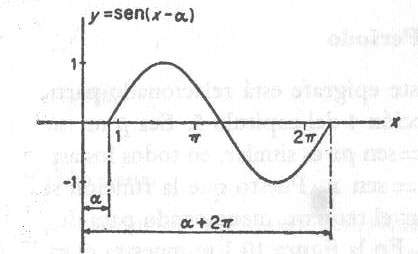
Si α es un numero real no negativo, α se puede representar en radianes de un águlo. El gráfico y=sen(x-α) es semejante al gráfico y= sen x en todos sus aspectos, excepto
en uno; esa diferencia se muestra en la figura. En lugar de intersecar el eje x en los puntos {0 ± nπ}, esta curva lo interseca en los puntos {α ± nπ}. Se describe este gráfico como un despplazamiento de la función seno α unidades a la derecha sobre el eje x
Segunda propiedad es la amplitud
Sea m un número real no negativo. El grafico y= m sen x, es similar en todos los aspectos menos en uno a y= sen x, como se observa en la figura.Cada ordenada de
la función es igual a la ordenada de y=sen x multiplicada por m, será mayor o menor que esta dependiendo que m sea mayor o menos que uno. La ordenada máxima positiva se llama amplitud de la función, como sen x tien su valor máximo en uno, la amplitud de m sen x será m.
Tercera propiedad es el período
Si p es un número real positivo. El gráfico de y=sen px, es similar a y=sen x excepto en uno del gráfico y=sen x. La función y=sen x tiene período 2π, se cumple por ser el seno una función períodica que sen px tiene período 2π/p
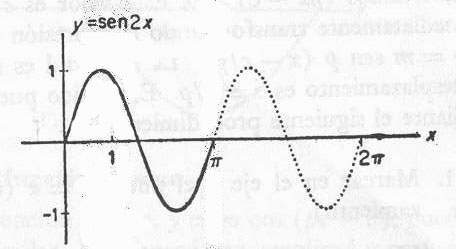
Analizamos si p=2
Grafico para p=2
Si p=1/2
Si p<1 se dilata y si p>1 se contrae
Generalizando
Generalizando los tres casos analizados anteriormente se llega a la función:
y=m f(px-α)
y la misma permite describir numerosos fenómenos físicos, llamados oscilaciones armónicas, siendo f definido tanto para el seno como para e coseno o sea.
El tamaño de la Tierra
Durante casi 1000 años después de la época de Alejandro Magno, la ciudad de Alejandría cerca de la desembocadura del Nilo, fue centro de la cultura por excelencia. Alrededor del año 300 (adne) se fundó allí una universidad y una gran biblioteca, donde se acumularon muchos de los escritos y observaciones del mundo antiguo. Arquímides, Euclides, Tolomeo y probablemente Hiparco, estuvieron estrechamente ligados a la universidad, junto con otros hombres de ciencia menos conocidos, como Eratóstenes (Griego 275-194 adne), e cual asumió el cargo de bibliotecario de la universidad durante un largo período.
Muchos años de la época de Eratóstenes existían argumentos convincentes que la tierra era esférica.
Dichos argumentos eran:
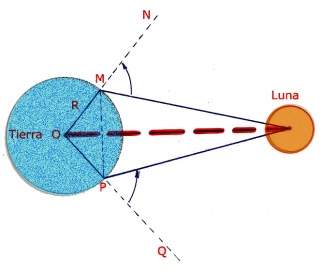
- La sombra que la Tierra proyecta sobre la Luna durate un eclipse aparece en forma circular. # Un cambio relativamente pequeño de la posición norte-sur sobre la superficie de la Tierra produce una variación apreciable en la altura de ciertas estrellas en el horizonte. Basado en esto Eratóstenes dio un método, usando trigonometría, para calcular el tamaño de la tierra.
Eratóstenes obtuvo antecedentes sobre un fenómeno no usual en un pozo profundo cerca de Siena, que por estimados se hallaba a unas 500 millas del sur de Alejandría.
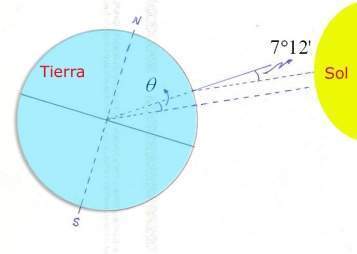
Un día del año al medio día la luz del sol penetraba verticalmente en el pozo, produciéndose reflejo en el agua. Él razonó que al ocurrir este fenómeno, el Sol, el pozo y el centro de la Tierra debían estar en línea recta. También observó que al mismo tiempo una columna vertical en Alejandría proyectaba una sombra que indicaba que el astro se encontraba a 7˚ 12´ al sur del cenit. Asumiendo que Alejandría y Siena, se encontraban en el mismo meridiano y que los rayos del Sol son paralelos determinó la circunferencia de la Tierra.
Conociendo que el ángulo que se forma desde el centro de la Tierra hasta las dos ciudades es de 7 12´ y que a ese ángulo le corresponde el arco de 500 millas de longitud, Dedujo que la circunferencia C estaría dada por la ecuación
,pero como una milla es aproximadamente, 1,6 Km. y un grado es 60 min. se obtiene que 7˚12´ es igual a 7,2˚ entonces
Lo que significo un gran paso dado que la longitud del ecuador es de 40 076.594Km
Fuentes
- Elementos de trigonometría plana de Henry Sharp Jr.
- Matemática 10mo grado de Dr Luís Campistrous Pérez y colectivo de autores.