Diferencia entre revisiones de «Multiplicación»
(Página creada con '{{Desarrollo}} {{Definición|Nombre=Multiplicación|imagen=Principalne.jpg|concepto=Operación inversa de la división}} == Multiplicación == <br> == Véase tambié...') (Etiqueta: Artículo sin Fuentes o Bibliografía o Referencias o Enlaces externos) |
(Agregué la imagen de la tabla de multiplicar) |
||
| (No se muestran 13 ediciones intermedias de 5 usuarios) | |||
| Línea 1: | Línea 1: | ||
| − | + | {{Definición | |
| + | |Nombre=Multiplicación | ||
| + | |imagen=Multip_plantilla.JPG | ||
| + | |concepto=Operación inversa de la [[división]]}} | ||
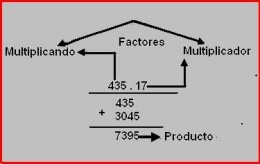
| − | + | '''Multiplicación'''. Es una [[suma]] abreviada en donde un [[número]] (primer factor o multiplicando) se repite varias veces (tantas como indique el segundo factor o multiplicador). | |
| + | == Definición == | ||
| + | La multiplicación de dos números enteros n y m se expresa como: | ||
| + | m x n o m.n | ||
| − | <br> | + | Ésta no es más que una forma de simbolizar la expresión: ''Sumar '''m''' a sí mismo '''n''' veces''. |
| + | |||
| + | == Notación == | ||
| + | |||
| + | La multiplicación se indica con el aspa (×) o el punto medio (•). | ||
| + | |||
| + | En ausencia de estos caracteres se suele emplear el asterisco (*), sobre todo en [[Computación|Computación]] (este uso tiene su origen en "''[[Fortran|FORTRAN]]''"), pero está desaconsejado en otros ámbitos y sólo debe utilizarse cuando no hay otra alternativa. A veces se utiliza la [[letra]] equis (x), pero esto es desaconsejable porque crea una confusión innecesaria con la letra que normalmente se asigna a una incógnita en una ecuación. | ||
| + | |||
| + | Por último, se puede omitir el signo de multiplicación a menos que se multipliquen números o se pueda generar confusión sobre los nombres de las incógnitas, constantes o funciones (por ejemplo, cuando el nombre de alguna incógnita tiene más de una letra y podría confundirse con el producto de otras dos). | ||
| + | |||
| + | También suelen utilizarse signos de agrupación como paréntesis (), corchetes ([]) o llaves ({ }). Esto mayormente se utiliza para multiplicar [[números negativos]] entre sí o por números positivos. La multiplicación se indica con el signo se indica con un punto. | ||
| + | |||
| + | En los casos que los factores sean letras no se pone ningún signo entre ellos: '''ab''' representa '''''a . b''''', si se trata de una multiplicación de un [[número]] por una [[letra]]: Ejemplo '''5a''' quiere decir '''''5 . a''''' | ||
| + | |||
| + | == Factor 1 == | ||
| + | |||
| + | Si de dos factores uno es igual a la unidad el producto es igual al otro factor. | ||
| + | |||
| + | En general: '''a . 1 = 1 . a = a''' | ||
| + | |||
| + | == Factor 0 == | ||
| + | |||
| + | Si de dos factores uno es igual a [[cero]], el producto es [[cero]] cualquiera que sea el otro factor. | ||
| + | |||
| + | En general: '''a . 0 = 0 . a = 0''' | ||
| + | |||
| + | == Multiplicación por números terminados en ceros == | ||
| + | |||
| + | Para multiplicar un [[número]] por la unidad seguida de [[cero]]s, basta con añadir a la derecha del número tantos ceros como sean los que acompañan a la unidad. | ||
| + | |||
| + | '''Ejemplo:''' | ||
| + | |||
| + | 96 x 100 = 9600 <br> | ||
| + | 23 x 10 = 230 | ||
| + | == <br> Leyes o principales propiedades de la multiplicación == | ||
| + | |||
| + | *'''I. ''''''Ley de uniformidad'''. La multiplicación de números respectivamente iguales da siempre el mismo resultado. Otro enunciado de esta ley equivalente al anterior: Si los dos miembros de una igualdad se multiplican por un mismo [[número]], la igualdad subsiste. Es decir que: | ||
| + | |||
| + | '''Si a = b, Resulta a c = b c''' | ||
| + | |||
| + | Un tercer enunciado, equivalente a los anteriores pero de mayor uso práctico: Si se multiplican ordenadamente varias igualdades, resulta otra igualdad. Es decir que: | ||
| + | |||
| + | Si '''a = b<br> c = d<br> e = f'''<br> | ||
| + | |||
| + | Resulta que '''a c e = b d f''' | ||
| + | |||
| + | *'''II Ley conmutativa'''. El producto de varios [[número]]s es el mismo cualquiera sea el orden en que se multipliquen. Más brevemente: El orden de los factores no altera el producto. | ||
| + | |||
| + | Generalizando: '''a b c = b a c = c b a ''' | ||
| + | |||
| + | *'''III Ley asociativa'''. Si en una multiplicación se sustituyen varios factores por su producto, el resultado no varía. | ||
| + | |||
| + | Generalizando: '''a b c d = a ( b c ) d = ( a b ) ( c d)''' | ||
| − | + | *'''IV Ley distributiva'''. Esta ley se refiere a la multiplicación de una [[suma]] o diferencia indicada por un [[número]]. | |
| − | + | Ley distributiva de la multiplicación con respecto a la adición. Para multiplicar una [[suma]] indicada por un [[número]] se puede multiplicar cada sumando por dicho [[número]] y sumar los productos obtenidos. | |
| − | |||
| − | |||
| − | |||
| + | Generalizando: '''( a + b ) n = a n + b n ''' | ||
| + | Y análogamente: | ||
| − | == | + | '''(a + b + c + d ) n = a n + b n + c n + d n''' |
| + | <br> | ||
| + | == Tabla de Multiplicar == | ||
| + | [[Archivo:Tabla de multiplicacion.png|centro]] | ||
| + | == Véase también == | ||
| + | *[[División]] | ||
| + | *[[Múltiplos y divisores de un número]] | ||
| + | *[[Divisibilidad]] | ||
| + | *[[Máximo Común Divisor]]<br> | ||
| + | == Fuentes == | ||
*Sócrates Rosell Franco. Aritmética. Volumen I. Segunda Edición. | *Sócrates Rosell Franco. Aritmética. Volumen I. Segunda Edición. | ||
<br> | <br> | ||
| − | + | </div> | |
[[Category:Teoría_elemental_de_los_números]] | [[Category:Teoría_elemental_de_los_números]] | ||
última versión al 07:40 11 may 2022
| ||||||
Multiplicación. Es una suma abreviada en donde un número (primer factor o multiplicando) se repite varias veces (tantas como indique el segundo factor o multiplicador).
Sumario
Definición
La multiplicación de dos números enteros n y m se expresa como: m x n o m.n
Ésta no es más que una forma de simbolizar la expresión: Sumar m a sí mismo n veces.
Notación
La multiplicación se indica con el aspa (×) o el punto medio (•).
En ausencia de estos caracteres se suele emplear el asterisco (*), sobre todo en Computación (este uso tiene su origen en "FORTRAN"), pero está desaconsejado en otros ámbitos y sólo debe utilizarse cuando no hay otra alternativa. A veces se utiliza la letra equis (x), pero esto es desaconsejable porque crea una confusión innecesaria con la letra que normalmente se asigna a una incógnita en una ecuación.
Por último, se puede omitir el signo de multiplicación a menos que se multipliquen números o se pueda generar confusión sobre los nombres de las incógnitas, constantes o funciones (por ejemplo, cuando el nombre de alguna incógnita tiene más de una letra y podría confundirse con el producto de otras dos).
También suelen utilizarse signos de agrupación como paréntesis (), corchetes ([]) o llaves ({ }). Esto mayormente se utiliza para multiplicar números negativos entre sí o por números positivos. La multiplicación se indica con el signo se indica con un punto.
En los casos que los factores sean letras no se pone ningún signo entre ellos: ab representa a . b, si se trata de una multiplicación de un número por una letra: Ejemplo 5a quiere decir 5 . a
Factor 1
Si de dos factores uno es igual a la unidad el producto es igual al otro factor.
En general: a . 1 = 1 . a = a
Factor 0
Si de dos factores uno es igual a cero, el producto es cero cualquiera que sea el otro factor.
En general: a . 0 = 0 . a = 0
Multiplicación por números terminados en ceros
Para multiplicar un número por la unidad seguida de ceros, basta con añadir a la derecha del número tantos ceros como sean los que acompañan a la unidad.
Ejemplo:
96 x 100 = 9600
23 x 10 = 230
Leyes o principales propiedades de la multiplicación
- 'I. 'Ley de uniformidad. La multiplicación de números respectivamente iguales da siempre el mismo resultado. Otro enunciado de esta ley equivalente al anterior: Si los dos miembros de una igualdad se multiplican por un mismo número, la igualdad subsiste. Es decir que:
Si a = b, Resulta a c = b c
Un tercer enunciado, equivalente a los anteriores pero de mayor uso práctico: Si se multiplican ordenadamente varias igualdades, resulta otra igualdad. Es decir que:
Si a = b
c = d
e = f
Resulta que a c e = b d f
- II Ley conmutativa. El producto de varios números es el mismo cualquiera sea el orden en que se multipliquen. Más brevemente: El orden de los factores no altera el producto.
Generalizando: a b c = b a c = c b a
- III Ley asociativa. Si en una multiplicación se sustituyen varios factores por su producto, el resultado no varía.
Generalizando: a b c d = a ( b c ) d = ( a b ) ( c d)
- IV Ley distributiva. Esta ley se refiere a la multiplicación de una suma o diferencia indicada por un número.
Ley distributiva de la multiplicación con respecto a la adición. Para multiplicar una suma indicada por un número se puede multiplicar cada sumando por dicho número y sumar los productos obtenidos.
Generalizando: ( a + b ) n = a n + b n
Y análogamente:
(a + b + c + d ) n = a n + b n + c n + d n
Tabla de Multiplicar
Véase también
Fuentes
- Sócrates Rosell Franco. Aritmética. Volumen I. Segunda Edición.