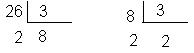Divisibilidad
| ||||||
Divisibilidad. Se refiere a la posibilidad de que dados dos números enteros a y b ( en particular dos números naturales) exista un número entero c tal que a = bc. En el caso de existir c, se dirá que a es divisible por b. Si tal hecho ocurre, se denota b | a, que se lee: b es divisor de a o b divide al número a. [1], [2]
Al tratar de la divisibilidad de los números no se dice nada sobre los diferentes valores que puede tomar al dividir a por b. Precisemos sea a = bc, y también a = bc1 que permite deducir
bc = bc1 ( a1) o lo mismo b(c-c1) = 0, en el supuesto de que b sea distinto de 0, c= c1. Se afirma la unicidad del cociente. Sin embargo, si b = 0, ciertamente, que a = 0 y la igualdad a1, se cumple para cualquier valor de c. De tal modo que 0 es únicamente divisible por 0, en tal caso el cociente es indeterminado. [3]
Sumario
Propiedades
- Reflexiva. Todo número es divisible por sí mismo. a|a.
- Transitiva. a|b y b|c implica a|c.
- Asimétrica. Si a|b y b|a, entonces a = b o bien a = -b.
- Si b | a y |b| >♀|a |, entonces a = 0.
- Si b | a y a diferente de 0, entonces |b| <♀|a |.
- Para que b | a es necesario y suficiente que |b| divida♀|a |. [4]
La última propiedad permite ver sólo el caso en que el divisor sea positivo. Además la divisibilidad de números enteros cualesquiera se restringe se a enteros no negativos.
Nomenclatura y partición
Centrándonos a los números no negativos se puede expresar de número primo, el número entero no negativo que tiene exactamente dos divisores: el mismo y 1. Por ejemplo: 11, 13, 14, 19, etc.
Un número que no es primo ni 1, se llama número compuesto. 4, 16, 64, 256, etc.
El número natural 1 no se considera primo.
En el conjunto de los números enteros no negativos se da la partición que incluye el conjunto de los números primos, el de los números compuestos y el conjunto unitario formado por 1.
Principios fundamentales
Los principios fundamentales de la divisibilidad son ciertas propiedades que sirven de base para deducir, para reunir las condiciones que debe reunir un número para ser divisible por otro.
I. Si un número divide a otros varios, divide a su suma.
Ejemplo: Investigar, sin hallarla, si la suma de 6; 12 y 15 será divisible por 3 .
Como 3 divide a 6, a 12, y a 15, podemos afirmar también que la suma de estos tres números será divisible por 3, aún sin saber a cuánto es igual la suma.
Respuesta: La suma será divisible por 3 por serlo 6; 12 y 15.
Prueba: 6 + 12 + 15 = 33
33: 3 = 11 Comprobando
II. Si un número divide a otros dos, divide a su diferencia.
Ejemplo: Averiguar si la diferencia entre 39 y 15 será divisible por 3 sin efectuar la resta.
Como 39 y 15 son múltiplos de 3 podemos asegurar que su diferencia también será múltiplo de 3.
Respuesta: Por ser 39 y 15 divisibles por 3, su diferencia también lo será.
III. Si un número divide a otro, divide a cualquier múltiplo de este.
Ejemplo: Investigar, sin efectuar la multiplicación, si 14 . 4 será divisible por 7
Como que 7 divide a 14 podemos asegurar que el producto de multiplicar 14 por 4 será también divisible por 7.
Respuesta: El producto será divisible por 7 por serlo 14.
Prueba: 14 . 4 = 56
56: 7 = 8 Comprobando.
IV. Si los sumandos no son divisibles por un número, la suma, sin embargo, podrá serlo de acuerdo a lo siguiente:
Si al dividir números dados entre otro número las divisiones no son exactas, pero la suma de los restos de estas divisiones es divisible exactamente por ese otro número, la suma de los números dados será también divisible por él.
Ejemplo: Investigar si la suma de 23, 53 y 15 será divisible por 7, sin efectuar la división. Dividimos cada uno de estos números por 7 para hallar los restos.
Y como la suma de los restos 2 + 4 + 1 = 7, la suma de los números 23; 53 y 15 será también múltiplo de 7, con toda seguridad. Respuesta: La suma de 23, 53 y 15 será divisible por 7 por serlo la suma de los restos obtenidos al dividir por 7 dichos números.
Prueba: 23 + 53 + 15 = 91
91 : 7 = 13 Comprobando.
V. Si al dividir dos números dados entre un tercero las divisiones no son exactas, pero los resto de esas divisiones son iguales, la diferencia de estos números será divisible por el tercero.
Ejemplo: Averiguar sin efectuar la resta, si la diferencia entre 26 y 8 será divisible por 3.
Como los restos son iguales, 2 = 2, podemos afirmar que la diferencia entre 26 y 8 será divisible por 3.
Respuesta: Como al dividir 26 y 8 por 3 los restos son iguales, la diferencia de 26 y 8 será divisible por 3.
Prueba: 26 – 8 = 18
18 : 3 = 6 comprobando.
VI. Si un número divide al dividendo y al divisor, divide al resto.
Ejemplo: Como 7 divide a 21 y a 35, el resto de 35: 21 tiene que ser divisible por 7. En efecto:
El resto es 14 que es múltiplo de 7.
VII. Si un número divide al divisor y al resto, divide también al dividendo.
En efecto, al dividir al divisor divide también al producto del divisor por el cociente de acuerdo con el tercer principio.
Criterios de divisibilidad
Los siguientes criterios nos permiten averiguar si un número es divisible por otro de una forma sencilla, sin necesidad de realizar una división:
| Número |
Criterio |
Ejemplo |
|
2 |
El número termina en cero(0) o cifra par |
476: porque "6" es par. |
|
3 |
La suma de sus cifras es un múltiplo de 3 |
534: porque 5+ 3+ 4 = 12 es múltiplo de 3 |
|
4 |
El número formado por las dos últimas cifras es un múltiplo de 4 |
5628: porque 28 es múltiplo de 4 |
|
5 |
La última cifra es 0 ó 5 |
560: porque termina en 0 |
|
6 |
El número es divisible por 2 y por 3 |
432: Ver criterios anteriores. |
|
7 |
Para números de 3 cifras: Al número formado por las dos primeras cifras se le resta la última multiplicada por 2. Si el resultado es múltiplo de 7, el número original también lo es. Para números de más de 3 cifras: Dividir en grupos de 3 cifras y aplicar el criterio de arriba a cada grupo. Sumar y restar alternativamente el resultado obtenido en cada grupo y comprobar si el resultado final es un múltiplo de 7. |
52176376: porque (37-12) - (17-12) + (5-4)= 25-5+1= 21 es múltiplo de 7. |
|
8 |
El número formado por las tres últimas cifras es un múltiplo de 8 |
42560: porque 560 es múltiplo de 8 |
|
9 |
La suma de sus cifras es múltiplo de 9 |
6534: porque 6+5+3+4= 18 es múltiplo de 9 |
|
10 |
La última cifra es 0 |
920: La última cifra es 0 |
| 11 |
Sumando las cifras (del número) en posición impar por un lado y las de posición par por otro. Luego se resta el resultado de ambas sumas obtenidas. Si el resultado es cero (0) o un múltiplo de 11, el número es divisible por este. Si el número tiene dos cifras será múltiplo de 11 si esas dos cifras son iguales. Si el número tiene dos cifras será múltiplo de 11 si esas dos cifras son iguales. |
42702: 4+7+2=13 • 2+0=2 • 13-2=11 → 42702 es múltiplo de 1166: porque las dos cifras son iguales. Entonces 66 es Múltiplo de 11 |
| 12 | El número es divisible por 3 y 4 |
216: Ver criterios anteriores |
| 13 |
Para números de más de 3 cifras: Dividir en grupos de 3 cifras, sumar y restar alternativamente los grupos de derecha a izquierda y aplicar el criterio de arriba al resultado obtenido. Si es múltiplo de 13, el número original también lo es. |
432549: porque 549-432 = 117 y luego 11 + 4•7 = 39 es múltiplo de 13. |
Referencias
- ↑ Enzo Gentile: Aritmética. Edición de OEA, Wáshington D.C.
- ↑ I. Vinogradov: Fundamentos de la teoría de números. Editorial Mir, Moscú ( 1977) 2da. edición, traduce E. Aparicio Bernardo, impreso en la URSS.
- ↑ N.N. Vorobiov: Criterios de divisibilidad. Editorial Mir, Moscú ( 1984) 2da. edición.
- ↑ Vorobiov. Op. cit.
Véase también
Fuentes
- Sócrates Rosell, F. Volumen I(Segunda Edición). Editorial Pedagógica.