Diferencia entre revisiones de «Regla de Barrow»
(Sustituyendo las imágenes que no se muestran, corrigiendo errores y añadiendo texto.) |
|||
| Línea 1: | Línea 1: | ||
{{Definición | {{Definición | ||
|nombre=Regla de Barrow | |nombre=Regla de Barrow | ||
| − | |imagen= | + | |imagen= Regla_Barrow.png |
|tamaño= | |tamaño= | ||
| − | |concepto= | + | |concepto= La integral definida de ''f'' en el intervalo ''[a,b]'' es ''F(b) - F(a)'', siendo ''F'' una primitiva de ''f'' (es decir, ''F' = f'' ). |
}}<div align="justify"> | }}<div align="justify"> | ||
| − | '''La Regla de Barrow''' | + | '''La Regla de Barrow''' establece que la [[integral definida]] de una [[Funciones continuas|función continua]] ''f(x)'' en el intervalo ''[a, b]'' es igual a la diferencia entre los valores que toma una [[función primitiva]] ''F(x)'' de ''f(x)'', en los extremos de dicho intervalo.<br> |
| − | <center>[[Image: Regla_Barrow. | + | <center>[[Image: Regla_Barrow.png]]<br></center> |
| − | La regla de Barrow se conoce como | + | La regla de Barrow también se conoce como el segundo [[teorema fundamental del cálculo]].<br> |
| − | + | ||
| − | + | Para resolver una integral definida de una función, es suficiente encontrar una [[Función primitiva|primitiva de la función]] y sustituir en ella los límites superior e inferior de integración y restar ambos valores.<br> | |
| − | Para resolver una integral definida de una función | + | === Ejemplos === |
| − | + | ||
| − | + | Aplicación de la Regla de Barrow para calcular las integrales definidas de ''x<sup>2</sup>-2x'' en los intervalos [-1, 0] | |
| − | <center>[[Image: | + | y [0,1]: |
| − | + | ||
| + | <center>[[Image: Regla_Barrow_ejemplo.png]]<br></center> | ||
| + | |||
| + | == Aplicaciones == | ||
| + | |||
| + | Las aplicaciones de la regla de Barrow son las aplicaciones de la propia integral definida. Esta regla se utiliza habitualmente para el cálculo de áreas encerradas entre la gráfica de funciones: | ||
| + | |||
| + | <center>[[Image: Barrow_area.png]]<br></center> | ||
| + | |||
| + | |||
| + | |||
== Fuentes == | == Fuentes == | ||
| − | + | *[https://www.matesfacil.com/matematicos/Barrow/Isaac-Barrow-primer-segundo-teorema-fundamental-calculo-regla-biografia.html Isaac Barrow: biografía y demostración del Teorema fundamental del cálculo] | |
| − | + | *[https://www.matesfacil.com/ejercicios-resueltos-integracion-areas.html Integrales definidas: cálculo de áreas] | |
| − | + | *Bronshtein I, Semendiaev K. Manual de Matemática para Ingenieros y Estudiantes. Editorial MIR. Moscú. 1988. | |
| + | *Ilín V, Pozniak E. Análisis Matemático. En tres tomos. Editorial MIR. Moscú. 1991. | ||
| + | *Piskunov, N. Cálculo Diferencial e Integral. Editorial MIR. Moscú. 1980. | ||
[[Category:Matemáticas]] | [[Category:Matemáticas]] | ||
Revisión del 11:46 21 ene 2017
| ||||||
La Regla de Barrow establece que la integral definida de una función continua f(x) en el intervalo [a, b] es igual a la diferencia entre los valores que toma una función primitiva F(x) de f(x), en los extremos de dicho intervalo.
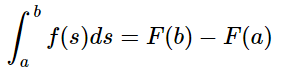
La regla de Barrow también se conoce como el segundo teorema fundamental del cálculo.
Para resolver una integral definida de una función, es suficiente encontrar una primitiva de la función y sustituir en ella los límites superior e inferior de integración y restar ambos valores.
Ejemplos
Aplicación de la Regla de Barrow para calcular las integrales definidas de x2-2x en los intervalos [-1, 0] y [0,1]:
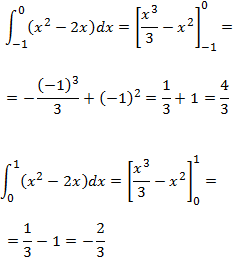
Aplicaciones
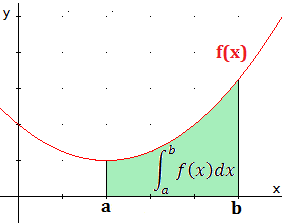
Las aplicaciones de la regla de Barrow son las aplicaciones de la propia integral definida. Esta regla se utiliza habitualmente para el cálculo de áreas encerradas entre la gráfica de funciones:
Fuentes
- Isaac Barrow: biografía y demostración del Teorema fundamental del cálculo
- Integrales definidas: cálculo de áreas
- Bronshtein I, Semendiaev K. Manual de Matemática para Ingenieros y Estudiantes. Editorial MIR. Moscú. 1988.
- Ilín V, Pozniak E. Análisis Matemático. En tres tomos. Editorial MIR. Moscú. 1991.
- Piskunov, N. Cálculo Diferencial e Integral. Editorial MIR. Moscú. 1980.
