Diferencia entre revisiones de «Ley de Lotka»
(Página creada con '{{Desarrollo}} <div align="justify"> {{Definición |nombre=Ley de Lotka |imagen= |tamaño= |concepto= }}'''Ley de Lotka.''' Es una distribución de probabilidades discreta que ...') |
|||
| Línea 14: | Línea 14: | ||
De los datos observados, formuló una ley empírica describiendo la productividad de los autores en una población dada: el número de químicos (N) que publican publicaciones químicas es proporcional a 1/n2 de esos químicos. Derek de Solla Price reescribió la ley así: la mitad de los documentos científicos son contribución de la raíz cuadrada del total del número de autores científicos. | De los datos observados, formuló una ley empírica describiendo la productividad de los autores en una población dada: el número de químicos (N) que publican publicaciones químicas es proporcional a 1/n2 de esos químicos. Derek de Solla Price reescribió la ley así: la mitad de los documentos científicos son contribución de la raíz cuadrada del total del número de autores científicos. | ||
| − | En una discusión sobre la ley de Lotka, William Gray Potter dijo que el artículo en el cual Lotka da a conocer su ley no fue publicado sino hasta 1941, | + | En una discusión sobre la ley de Lotka, William Gray Potter dijo que el artículo en el cual Lotka da a conocer su ley no fue publicado sino hasta 1941, su distribución no fue llamada ''ley de Lotka'' hasta 1949 y ningún intento fue hecho para evaluar la aplicabilidad de la ley de Lotka en otras disciplinas hasta 1973. |
Alfred Lotka fue el primero en proporcionar un modelo de distribución tamaño/frecuencia, estudiando la productividad de los autores de la química, cediendo las bases para desarrollar lo que hoy se conoce como la Ley cuadrada inversa de Lotka. | Alfred Lotka fue el primero en proporcionar un modelo de distribución tamaño/frecuencia, estudiando la productividad de los autores de la química, cediendo las bases para desarrollar lo que hoy se conoce como la Ley cuadrada inversa de Lotka. | ||
| − | |||
A pesar del esfuerzo de Lotka muchos autores coinciden que la Ley no es estadísticamente exacta, pero sin duda alguna para la época y la posterioridad la Ley de productividad de Lotka ha significado un avance en el menester diario por medir los resultados de la actividad de la comunidad científica. | A pesar del esfuerzo de Lotka muchos autores coinciden que la Ley no es estadísticamente exacta, pero sin duda alguna para la época y la posterioridad la Ley de productividad de Lotka ha significado un avance en el menester diario por medir los resultados de la actividad de la comunidad científica. | ||
| + | == Descripción == | ||
| + | |||
| + | La Ley de Lotka expresa, que el mayor número de autores publican el menor número de trabajos, mientras que el menor número de autores publica un mayor número de trabajos, siendo este el grupo más prolífico. | ||
| + | *Es la ley de la distribución de los autores según su productividad. | ||
| + | *Propuesta por Lotka y dada a conocer por Price. | ||
| + | *Es formalmente equivalente a la Ley de Pareto de la Economía. | ||
| + | *Verbalmente se enuncia diciendo que: "El número de autores, '''''An''''', que publican '''''n''''' trabajos sobre una materia es inversamente porporcional a '''''n''''' al cuadrado". Se formula de la siguiente manera:[[Archivo:Expresión_de_la_Ley_de_Lotka.jpg]] | ||
| + | |||
| + | De dónde An es el número de trabajos que corresponden a determinado número de autores aplicando la Ley de Lotka, A1 son el número de trabajos elaborados por un único autor n2 es el número de autores para el cual queremos calcular los trabajos que le corresponderían aplicando la Ley del crecimiento exponencial elevado al cuadrado. | ||
| + | *Implica que muy pocos autores publican la mayoría de los trabajos: Para una productividad alta ('''''n''''' grande), el número de autores, '''''An''''', es bajo, ya que ambas variables son inversas. | ||
| + | *Nunca es exactamente cuadrática, pero se puede generalizar diciendo que el número de trabajos firmados se eleva a un exponente '''''m''''', que puede ser algo diferente a 2. | ||
== Fuente == | == Fuente == | ||
*''Bibliometría''. Tomado de ''Bibliotecas''. Vol. VIII, No.1. Enero-Junio, 1990 pp. 1-11. Disponible en: http://www.repositorio.una.ac.cr/bitstream/handle/11056/2612/recurso_708.pdf?sequence=1. Consultado el 13 de agosto de 2014. | *''Bibliometría''. Tomado de ''Bibliotecas''. Vol. VIII, No.1. Enero-Junio, 1990 pp. 1-11. Disponible en: http://www.repositorio.una.ac.cr/bitstream/handle/11056/2612/recurso_708.pdf?sequence=1. Consultado el 13 de agosto de 2014. | ||
[[Categoría:Ciencias de la Información]][[Categoría:Bibliometría]][[Categoría:Leyes bibliométricas]] | [[Categoría:Ciencias de la Información]][[Categoría:Bibliometría]][[Categoría:Leyes bibliométricas]] | ||
Revisión del 14:36 13 ago 2014
| ||
Reseña
En 1926 Alfred Lotka estuvo interesado en conocer cómo el aporte de diferentes figuras reconocidas en las distintas tendencias del quehacer de la actividad generadora del conocimiento, cooperaba al desarrollo de las Ciencias, e incurre en un estudio de la producción de artículos en química y física, analizando la productividad de los científicos de forma individual en los índices del Chemical Abstracts por 20 años (1907–1916); comienza por la realización de un conteo de la incidencia de cada autor y la cantidad de veces que se encontraban, por lo que logró contabilizar 6891 nombres que comenzaban con las letras A y B.
De los datos observados, formuló una ley empírica describiendo la productividad de los autores en una población dada: el número de químicos (N) que publican publicaciones químicas es proporcional a 1/n2 de esos químicos. Derek de Solla Price reescribió la ley así: la mitad de los documentos científicos son contribución de la raíz cuadrada del total del número de autores científicos.
En una discusión sobre la ley de Lotka, William Gray Potter dijo que el artículo en el cual Lotka da a conocer su ley no fue publicado sino hasta 1941, su distribución no fue llamada ley de Lotka hasta 1949 y ningún intento fue hecho para evaluar la aplicabilidad de la ley de Lotka en otras disciplinas hasta 1973.
Alfred Lotka fue el primero en proporcionar un modelo de distribución tamaño/frecuencia, estudiando la productividad de los autores de la química, cediendo las bases para desarrollar lo que hoy se conoce como la Ley cuadrada inversa de Lotka.
A pesar del esfuerzo de Lotka muchos autores coinciden que la Ley no es estadísticamente exacta, pero sin duda alguna para la época y la posterioridad la Ley de productividad de Lotka ha significado un avance en el menester diario por medir los resultados de la actividad de la comunidad científica.
Descripción
La Ley de Lotka expresa, que el mayor número de autores publican el menor número de trabajos, mientras que el menor número de autores publica un mayor número de trabajos, siendo este el grupo más prolífico.
- Es la ley de la distribución de los autores según su productividad.
- Propuesta por Lotka y dada a conocer por Price.
- Es formalmente equivalente a la Ley de Pareto de la Economía.
- Verbalmente se enuncia diciendo que: "El número de autores, An, que publican n trabajos sobre una materia es inversamente porporcional a n al cuadrado". Se formula de la siguiente manera:
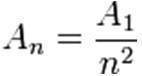
De dónde An es el número de trabajos que corresponden a determinado número de autores aplicando la Ley de Lotka, A1 son el número de trabajos elaborados por un único autor n2 es el número de autores para el cual queremos calcular los trabajos que le corresponderían aplicando la Ley del crecimiento exponencial elevado al cuadrado.
- Implica que muy pocos autores publican la mayoría de los trabajos: Para una productividad alta (n grande), el número de autores, An, es bajo, ya que ambas variables son inversas.
- Nunca es exactamente cuadrática, pero se puede generalizar diciendo que el número de trabajos firmados se eleva a un exponente m, que puede ser algo diferente a 2.
Fuente
- Bibliometría. Tomado de Bibliotecas. Vol. VIII, No.1. Enero-Junio, 1990 pp. 1-11. Disponible en: http://www.repositorio.una.ac.cr/bitstream/handle/11056/2612/recurso_708.pdf?sequence=1. Consultado el 13 de agosto de 2014.