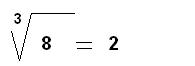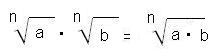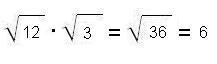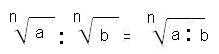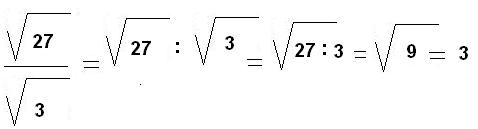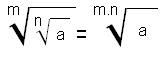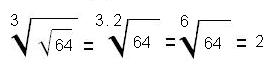Diferencia entre revisiones de «Radicación»
(→Equivalencias operatorias: Las cargas se arreglan en el camino, quizás hay que romper patrones rutinarios.) |
(→Equivalencias operatorias: Se facilita la escritura de raíces y se maneja propiedades de logaritmo en cualquiera base.) |
||
| Línea 45: | Línea 45: | ||
==Equivalencias operatorias== | ==Equivalencias operatorias== | ||
| − | * En forma de potencia Si la raíz enésima de a es x, se puede escribir: a<sup>1/n</sup> = x. Como aplicación, si los catetos de un triángulo rectángulo son 7 y 24 m su hipotenusa es: | + | * En forma de potencia Si la raíz enésima de a es x, se puede escribir: a<sup>1/n</sup> = x. |
| + | |||
| + | Como aplicación, si los catetos de un triángulo rectángulo son 7 y 24 m su hipotenusa es: | ||
::: h = (7<sup>2</sup> +24<sup>2</sup>)<sup>1/2</sup> = 25 m. | ::: h = (7<sup>2</sup> +24<sup>2</sup>)<sup>1/2</sup> = 25 m. | ||
| Línea 52: | Línea 54: | ||
::: r = (3V/4π)<sup>1/3</sup> | ::: r = (3V/4π)<sup>1/3</sup> | ||
| + | * a<sup>1/n</sup> = x, si sólo si 1/n log<sub>b</sub> a = log<sub>b</sub> x | ||
| + | |||
| + | ::: 8<sup>1/3</sup> = 2 s.s.s. 1/3 log<sub>4</sub> 8 = log<sub>4</sub> 2 s.s.s. 1/3 por 3/2 = 1/2. | ||
== Fuentes == | == Fuentes == | ||
Revisión del 23:51 8 ene 2016
| ||||||
Radicación o extracción de la raíz. Es una operación aritmética que tiene por objeto, dados una potencia de un número y el exponente, hallar el número ( o específicamente la base). El signo que se usa se llama signo radical ( una alteración de la letra latina r); en su abertura se coloca el exponente, que se denomina índice o grado de la raíz y debajo de la raya horizontal se coloca la potencia, que se llama o cantidad subradical o radicando. El resultado obtenido se llama raíz. Se trata de resolver la ecuación xn = a, que se alcanza con precisiones sobre el valor admisible de a y la paridad de n. Precisamente, la búsqueda de resolver tal ecuación, permitió ampliar los números racionales, al resolver , un caso histórico, la raíz cuadrada de 2; otro caso resolver la ecuación x2 = -1, que forzó crear la unidad imaginaria y los números complejos.
Ejemplo, en: 
El 3 es el índice o grado de la raíz, el 8 es la cantidad o número subradical y el 2 es la raíz.
En general: en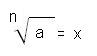 
, n es el índice o grado de la raíz, a es el número subradical, y x es la raíz enésima de a, que tiene que cumplir la condición: xn = a.
Cuando el índice es 2, no se escribe y se lee: raíz cuadrada de....
Ejemplo: 
se lee raíz cuadrada de 9.
Sumario
Raíz de un producto
La raíz de un producto de factores es igual al producto de las raíces de los factores:
Ejemplo:
Raíz de un cociente
La raíz de una fracción es igual al cociente de la raíz del numerador entre la raíz del denominador:
Ejemplo:
Raíz de una raíz
Para calcular la raíz de una raíz se multiplican los índices de las raíces y se conserva la cantidad subradical:
Ejemplo:
Equivalencias operatorias
- En forma de potencia Si la raíz enésima de a es x, se puede escribir: a1/n = x.
Como aplicación, si los catetos de un triángulo rectángulo son 7 y 24 m su hipotenusa es:
- h = (72 +242)1/2 = 25 m.
Si el volumen de una esfera es V m3, entonces su radio r, se obtiene con la fórmula
- r = (3V/4π)1/3
- a1/n = x, si sólo si 1/n logb a = logb x
- 81/3 = 2 s.s.s. 1/3 log4 8 = log4 2 s.s.s. 1/3 por 3/2 = 1/2.
Fuentes
- Libro de texto Matemática 10 mo grado.
- Rosell Sócrates, F. Volumen I(Segunda Edición). Editorial Pedagógica.
- E. T. Bell. Historia de las matemáticas
