Diferencia entre revisiones de «Bifurcación tridente»
m (→Forma) |
m |
||
| Línea 1: | Línea 1: | ||
'''Bifurcación tridente''' | '''Bifurcación tridente''' | ||
| − | En [[Matemáticas|matemática]], una '''bifurcación tridente''' (en inglés “pitchfork”) es un tipo de bifurcación '''local'''. Las bifurcaciones tridente pueden ser '''supercríticas''' o '''subcríticas'''.<ref> Carlos Fernández Pérez, Francisco José Vázquez Hernández, José Manuel Vegas Montaner, Ecuaciones diferenciales y en diferencias. Editorial Paraninfo, 2003, páginas 331 y 673</ref> | + | En [[Matemáticas|matemática]], una '''bifurcación tridente''' (en inglés “pitchfork”) es un tipo de bifurcación '''local''' de una ecuación diferencial de un [[sistema dinámico]]. Las bifurcaciones tridente pueden ser '''supercríticas''' o '''subcríticas'''.<ref> Carlos Fernández Pérez, Francisco José Vázquez Hernández, José Manuel Vegas Montaner, Ecuaciones diferenciales y en diferencias. Editorial Paraninfo, 2003, páginas 331 y 673</ref> |
En los [[sistemas dinámicos]] continuos descritos por una [[ecuación diferencial ordinaria]], bifurcaciones tridente se producen en sistemas con simetría. Es decir, que esta bifurcación está relacionada a simetrías del sistema. Por ejemplo, en sistemas que tienen una simetría espacial entre puntos fijos, izquierdo y derecho, estos tienden a aparecer y desaparecer en pares simétricos (ejemplo: análisis de pandeo de un comprimido haz recto). <ref>http://www.autofemsoft.com/examples/es/buckling_analysis_of_a_compres_surf.html</ref> | En los [[sistemas dinámicos]] continuos descritos por una [[ecuación diferencial ordinaria]], bifurcaciones tridente se producen en sistemas con simetría. Es decir, que esta bifurcación está relacionada a simetrías del sistema. Por ejemplo, en sistemas que tienen una simetría espacial entre puntos fijos, izquierdo y derecho, estos tienden a aparecer y desaparecer en pares simétricos (ejemplo: análisis de pandeo de un comprimido haz recto). <ref>http://www.autofemsoft.com/examples/es/buckling_analysis_of_a_compres_surf.html</ref> | ||
| Línea 39: | Línea 39: | ||
==Véase también== | ==Véase también== | ||
*[[Bifurcaciones de ecuaciones diferenciales]] | *[[Bifurcaciones de ecuaciones diferenciales]] | ||
| − | *[[ | + | *[[Bifurcación silla-nodo]] |
==Referencias== | ==Referencias== | ||
Revisión del 11:42 9 jul 2016
Bifurcación tridente
En matemática, una bifurcación tridente (en inglés “pitchfork”) es un tipo de bifurcación local de una ecuación diferencial de un sistema dinámico. Las bifurcaciones tridente pueden ser supercríticas o subcríticas.[1]
En los sistemas dinámicos continuos descritos por una ecuación diferencial ordinaria, bifurcaciones tridente se producen en sistemas con simetría. Es decir, que esta bifurcación está relacionada a simetrías del sistema. Por ejemplo, en sistemas que tienen una simetría espacial entre puntos fijos, izquierdo y derecho, estos tienden a aparecer y desaparecer en pares simétricos (ejemplo: análisis de pandeo de un comprimido haz recto). [2]
Definición
Si la ecuación diferencial ordinaria dx/dt = f(x, C), descrita por un solo parámetro C de la función f(x, C), con C siendo un miembro o elemento de los números reales (C ∈ R), y f(x, C) es una función impar a lo cual:
f(-x, C) = - f(x, C), y ademas:
df/dx (0, Co) = 0; d2f/dx2 (0, Co) = 0;
d3f/dx3 (0, Co) no es cero;
df/dc (0, Co) = 0; d2f/dcdx (0, Co) no es cero
entonces la ecuación diferencial tiene una bifurcación tridente en el punto fijo (0, Co) [3]
Estabilidad
d3f/dx3 (0, Co) > 0 → subcritico
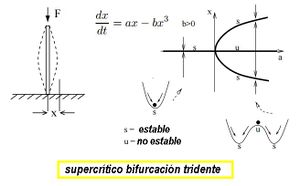
d3f/dx3 (0, Co) < 0 → supercritico [4]
Forma
La forma normal es:
dx/dt = Cx ∓ x3
La forma normal de una bifurcación es un sistema dinámico simple que es equivalente a todos los sistemas que muestran esta bifurcación.[5]
Ejemplo 1
Bifurcaciones tridente son comunes en los sistemas físicos que poseen simetría. Un ejemplo es el puntal de Euler (“Euler strut” en ingles).
En el puntal de Euler se aplica una carga cada vez mayor a un puntal vertical, hasta que finalmente hebillas. Derecha e izquierda pandeo son equivalentes y se aplica la simetría de función impar. Un análisis muestra que el sistema tiene una bifurcación tridente supercrítico en el punto de pandeo.
Véase también
Referencias
- ↑ Carlos Fernández Pérez, Francisco José Vázquez Hernández, José Manuel Vegas Montaner, Ecuaciones diferenciales y en diferencias. Editorial Paraninfo, 2003, páginas 331 y 673
- ↑ http://www.autofemsoft.com/examples/es/buckling_analysis_of_a_compres_surf.html
- ↑ Weisstein, Eric W. "Pitchfork Bifurcation." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/PitchforkBifurcation.html
- ↑ Steven Strogatz, "Non-linear Dynamics and Chaos: With applications to Physics, Biology, Chemistry and Engineering", Perseus Books, 2000.
- ↑ Guckenheimer, John; Holmes, Philip (1983), Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields, Springer, Section 3.3, ISBN 0-387-90819-6.