Diferencia entre revisiones de «Pentágono (geometría)»
| Línea 6: | Línea 6: | ||
|tamaño= 150 px | |tamaño= 150 px | ||
|concepto= Polígono que tiene cinco lados, los cuales pueden ser iguales o diferentes. | |concepto= Polígono que tiene cinco lados, los cuales pueden ser iguales o diferentes. | ||
| − | }} | + | }} |
| − | + | En geometría, se denomina '''pentágono''' a un [[polígono]] de cinco lados y cinco vértices. Los pentágonos pueden ser regulares o irregulares. | |
| − | |||
== Elementos == | == Elementos == | ||
| − | + | ||
* Ángulos de un pentágono. | * Ángulos de un pentágono. | ||
* Diagonales de un pentágono. | * Diagonales de un pentágono. | ||
| Línea 27: | Línea 26: | ||
== Área == | == Área == | ||
| − | |||
| − | |||
El área de esta figura se calcula mediante la fórmula: | El área de esta figura se calcula mediante la fórmula: | ||
| Línea 35: | Línea 32: | ||
== Perímetro == | == Perímetro == | ||
| + | |||
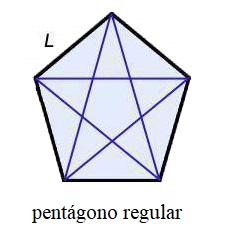
| + | [[Archivo:Pentagono_regular_con_sus_diagonales.jpg|miniatura|Un pentágono regular, con sus diagonales.]] | ||
El perímetro de esta figura se calcula mediante la fórmula: | El perímetro de esta figura se calcula mediante la fórmula: | ||
| Línea 44: | Línea 43: | ||
La apotema ''a'' satisface la ecuación 4a<sup>2</sup> = 4R<sup>2</sup> -l<sup>2</sup> | La apotema ''a'' satisface la ecuación 4a<sup>2</sup> = 4R<sup>2</sup> -l<sup>2</sup> | ||
| + | |||
| + | == Pentágonos regulares == | ||
| + | |||
| + | El pentágono regular es aquel que tiene todos sus lados iguales. | ||
== Pentágonos irregulares == | == Pentágonos irregulares == | ||
| − | [[ | + | |
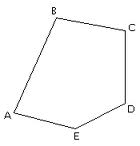
| + | [[Archivo:pentai.jpg|miniatura|Un pentágono irregular, o sea, que tiene sus lados desiguales.]] | ||
| + | |||
El pentágono irregular es el que tiene sus lados diferentes. | El pentágono irregular es el que tiene sus lados diferentes. | ||
Revisión del 18:38 26 ago 2021
| ||||||
En geometría, se denomina pentágono a un polígono de cinco lados y cinco vértices. Los pentágonos pueden ser regulares o irregulares.
Sumario
Elementos
- Ángulos de un pentágono.
- Diagonales de un pentágono.
- Apotemas de un pentágono regular. Estos elementos son 5.
Propiedades
- Los lados son iguales
- Los ángulos internos son congruentes.
- Cada ángulo interno mide 108 grados.
- La suma de los ángulos internos de un pentágono regular es de 540° ó 3π radianes.
- La apotema es igual al radio del círculo inscrito.
- De cada ángulo parten dos diagonales exactamente.
- El ángulo central es 360/5 = 72º
Área
El área de esta figura se calcula mediante la fórmula:
Área del pentágono = (perímetro.apotema) / 2
Perímetro
El perímetro de esta figura se calcula mediante la fórmula:
Perímetro = 5 · l
Apotema
Sean l = lado; a = apotema y R = radio del círculo circunscrito
La apotema a satisface la ecuación 4a2 = 4R2 -l2
Pentágonos regulares
El pentágono regular es aquel que tiene todos sus lados iguales.
Pentágonos irregulares
El pentágono irregular es el que tiene sus lados diferentes.
Fuentes
- «polígonos», artículo publicado en mayo de 2007 en el sitio web Matemática Educativa (Blogspot).
- «Clasifiquemos los polígonos», artículo publicado en el sitio web Escolares.net.
- «Los nombres de los polígonos», artículo publicado en el sitio web Red Escolar.ILCE.edu.mx (México).