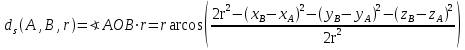Línea geodésica

Línea geodésica Concepto: Línea superficial que tiene la menor distancia entre dos puntos diferentes sobre la superficie de una esfera.

Línea geódesica. En Matemáticas, Álgebra, Geometría y más específicamente, Espacio métrico, Geometría análitica y Topología, dícese de la menor línea superficial que conecta a dos puntos desiguales en la superficie de una esfera, sustituyendo así la idea cartesiana de la recta por el arco de la línea geodésica que une a los puntos en cuestión.

Este tipo de lugar geométrico es de gran utilidad, pues planetas y estrellas suelen tener forma esférica, por lo que la determinación de distancias más realistas sobre sus superficies puede resolverse mediante la definición de la ortodroma o línea geodésica.

Definiciones.

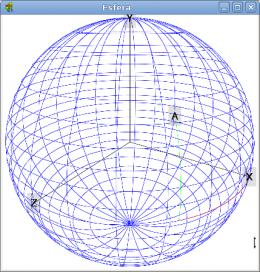
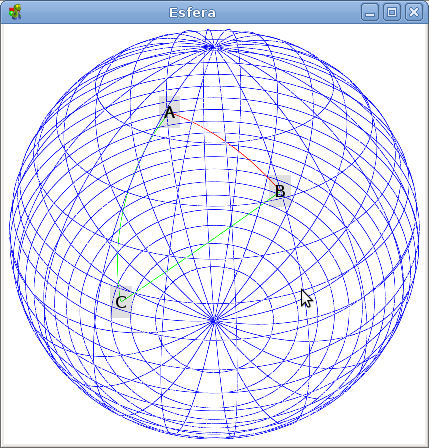
Sea una esfera sólida de centro O y radio r como se muestra en la figura siguiente:

• 

y dos puntos A=(x₀;y₀) y B=(x₁;y₁) localizados sobre la superficie de la esfera, se dice que el menor arco AB que conecta a ambos puntos sobre la esfera es la línea geodésica u ortodroma.

Cálculo de la longitud de la ortodroma.

Sea la esfera perfecta de centro en el origen de coordenadas O y radio r y dos puntos superficiales y donde son las longitudes de sus respectivos puntos respecto al eje x; son las latitudes correspondientes de A y B.

Traducidos a coordenadas euclideanas en el espacio los puntos y ; la amplitud del arco correspondiente a ese segmento es:

• 

Asumiendo que la función arcoseno devuelve la amplitud del ángulo en radianes, la longitud del arco entre dos puntos dadas sus coordenadas esféricas queda:

• 

Veáse también.

• Métrica esférica.
• Coordenada esférica.

Fuentes.

1. I. Bronshtein, K. Semendiaev. Manual de matemáticas para ingenieros y estudiantes. 2da Edición. Editorial MIR, Moscú. 1973.
2. Colectivo de autores. Matemática 11no grado. Editorial Pueblo y Educación, La Habana. 1989.
3. Distancia en Wikipedia. Revisado 5 de junio de 2012.