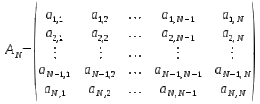¿No sabes por dónde empezar? Ayúdanos normalizando artículos.
¿Tienes experiencia? Crea alguno de estos artículos de actualidad.
Diferencia entre revisiones de «Matriz singular»
| Línea 6: | Línea 6: | ||
En este caso, el [[sistema de ecuaciones lineales]] asociado a dicha matriz no tiene solución o tiene infinas soluciones coincidentes. | En este caso, el [[sistema de ecuaciones lineales]] asociado a dicha matriz no tiene solución o tiene infinas soluciones coincidentes. | ||
| − | == Definiciones | + | == Definiciones == |
Dada la matriz cuadrada ''A'' de orden ''N'' se dice que es '''matriz singular''' cuando su determinante es cero. | Dada la matriz cuadrada ''A'' de orden ''N'' se dice que es '''matriz singular''' cuando su determinante es cero. | ||
| − | == Ejemplos | + | == Ejemplos == |
En la matriz ''A'': | En la matriz ''A'': | ||
| Línea 45: | Línea 45: | ||
* [[Determinante]]. | * [[Determinante]]. | ||
| − | == Fuentes | + | == Fuentes == |
* Colectivo de Autores. [[Álgebra lineal]]. [[Editorial Félix Valera]]. [[2003]]. | * Colectivo de Autores. [[Álgebra lineal]]. [[Editorial Félix Valera]]. [[2003]]. | ||
Revisión del 14:26 19 ene 2017
| ||||||
Matriz singular. Es la matriz cuadrada de orden N cuyo determinante es nulo.
En este caso, el sistema de ecuaciones lineales asociado a dicha matriz no tiene solución o tiene infinas soluciones coincidentes.
Sumario
[ocultar]Definiciones
Dada la matriz cuadrada A de orden N se dice que es matriz singular cuando su determinante es cero.
Ejemplos
En la matriz A:
| 1 | 2 | 3 |
| 4 | 5 | 6 |
| 7 | 8 | 9 |
al calcular su determinante:
- |A| = 1(5x9-8x6)-4(2x9-8x3)+7(2x6-5x3) = 1(45-48)-4(18-24)+7(12-15) = -3-4(-6)+7(-3) = -3+24-21 = 0,
se puede afirmar que A es una matriz singular.
En cambio la matriz M:
| 1 | 2 | 3 |
| 3 | 4 | 5 |
| 5 | 6 | 8 |
tiene |M|=-2, por lo que es no singular.
Véase también
Fuentes
- Colectivo de Autores. Álgebra lineal. Editorial Félix Valera. 2003.
- K. Ribnikov. Análisis Combinatorio. Editorial Mir Moscú. 1988.