Diferencia entre revisiones de «Circunferencia de los nueve puntos»
(corrijo) |
|||
| Línea 6: | Línea 6: | ||
}} | }} | ||
| − | ''' | + | La '''circunferencia de los nueve puntos''', |
| − | + | '''circunferencia de Feuerbach''' o | |
| − | + | '''circunferencia de Euler''' | |
| − | + | es la circunferencia que puede trazarse por puntos ligados a un [[triángulo]] escaleno no obtusángulo. | |
| + | |||
| + | Se la conoce con varios nombres: | ||
| + | * circunferencia de Feuerbach, tal como conocen en el mundo alemán<ref>Donaire Peña, Milton: ''Formas y números''.</ref> | ||
| + | * circunferencia de Euler, en el ámbito francés | ||
| + | * circunferencia de los nueve puntos, en el área anglosajona, [[Latinoamérica]], [[Rusia]], [[Japón]], [[India]] y [[China]]. | ||
| + | |||
| + | Su nombre, mencionando el cardinal de un conjunto de puntos, se debe a que la circunferencia atraviesa nueve puntos con nombre propio, seis de ellos sobre el mismo triángulo. Son los siguientes nueve puntos: | ||
| + | |||
| + | * Los tres centros de los tres lados del triángulo. | ||
| + | * Los tres pies de las alturas de tal triángulo. | ||
| + | * Los tres centros de cada uno de los segmentos que unen los tres vértices del triángulo con su ortocentro. | ||
| + | |||
== Síntesis histórica == | == Síntesis histórica == | ||
| − | |||
| − | Anteriormente, [[Carlos Brianchon]] y [[Juan-Victor Fernandes]] habían demostrado su existencia. Poco tiempo después de Feuerbach, Olry Terquem también demostró la existencia del círculo y reconoció además que los puntos medios de los segmentos determinados por los vértices del triángulo y el ortocentro, además están ubicados en la circunferencia (en la figura, los puntos: D F H). | + | Tradicionalmente, se adjudica al alemán [[Karl Feuerbach]] (1800-1934) el hallazgo de la circunferencia de los nueve puntos; sin embargo, lo que él encontró fue la circunferencia de los seis puntos, reconociendo que sobre ella se encuentran los puntos medios de los lados de un triángulo y los pies de las alturas (en la figura, los puntos: M N P y E G J). |
| + | |||
| + | Anteriormente, [[Carlos Brianchon]] y [[Juan-Victor Fernandes]] habían demostrado su existencia. Poco tiempo después de Feuerbach, el francés [[Olry Terquem]] (1782-1862) también demostró la existencia del círculo y reconoció además que los puntos medios de los segmentos determinados por los vértices del triángulo y el ortocentro, además están ubicados en la circunferencia (en la figura, los puntos: D F H). | ||
=== Denominación === | === Denominación === | ||
| − | |||
| − | ==Proposición== | + | Poncelet la llamó «circunferencia de los nueve puntos», nombre mayormente empleado en los países de habla inglesa. Algunos geómetras franceses la llaman «círculo de Euler» (o «circunferencia de Euler») y los geómetras teutones la denominan «circunferencia de Feuerbach», y en México, «circunferencia de los nueve puntos» (sic).<ref>Eves, Howard (1969): ''Estudio de las geometrías I'' (pág. 126). México: Uteha, 1969. ISBN 968-438-780-6.</ref> |
| − | Los puntos que bisecan los lados, los pies de las alturas también los puntos que bisecan los segmentos que conectan los vértices con el ortocentro de todo triángulo pertenecen a una misma circunferencia <ref>Levi S. '' | + | |
| + | [[Charles Wexler]] lo presenta como un teorema notable de geometría moderna e indica sus propiedades.<ref>Wexler, Charles (1977): ''Geometría analítica. Un enfoque vectorial'' (pág. 104). Barcelona (Cataluña): Montaner y Simon, 1977. ISBN 84-274-0394-1.</ref> | ||
| + | Pero en la obra de Levi Shively (1953),<ref name=Shively/> en la primera edición en castellano, en Latinoamérica, ya se conocía con el nombre de la «circunfrencia de los nueve puntos».<ref>La primera edición en castellano de Howard Eves data en 1969; podría ser una llevada de agua para su molino de parte de los traductores.</ref> | ||
| + | |||
| + | == Proposición == | ||
| + | |||
| + | Los puntos que bisecan los lados, los pies de las alturas también los puntos que bisecan los segmentos que conectan los vértices con el ortocentro de todo triángulo pertenecen a una misma circunferencia.<ref name=Shively>Shively, Levi S. (1953): ''Introducción a la geometría moderna''.</ref> | ||
===Demostación=== | ===Demostación=== | ||
| − | Consideremos las alturas del triángulo ABC: AE, BG y CJ (véase la figura). El triángulo GEJ es el triángulo | + | Consideremos las alturas del triángulo ABC: AE, BG y CJ (véase la figura). El triángulo GEJ es el triángulo «órtico» del triángulo ABC, y el punto I es el ortocentro del triángulo ABC. Las alturas de este, son las bisectrices de los ángulos internos de aquel. Los lados del triángulo ABC son las bisectrices exteriores del triángulo GEJ. |
Las bisectrices del ángulo JGE cortan a la mediatriz del lado opuesto, EJ en los puntos F y N que se hallan sobre la circunferencia circunscrita c (descrito en el artículo de la [[bisectriz]] de un ángulo). | Las bisectrices del ángulo JGE cortan a la mediatriz del lado opuesto, EJ en los puntos F y N que se hallan sobre la circunferencia circunscrita c (descrito en el artículo de la [[bisectriz]] de un ángulo). | ||
| Línea 29: | Línea 47: | ||
Observemos que los triángulos ACJ y ACE son triángulos rectángulos teniendo ambos al lado AC como hipotenusa. Se sigue que los cuatro puntos A, C, E y J son concíclicos y el centro de la circunferencia que los contiene se halla sobre la intersección de la hipotenusa AC con la mediatriz del segmento EJ, esto es, el punto N. Se sigue que N es punto medio del segmento AC. | Observemos que los triángulos ACJ y ACE son triángulos rectángulos teniendo ambos al lado AC como hipotenusa. Se sigue que los cuatro puntos A, C, E y J son concíclicos y el centro de la circunferencia que los contiene se halla sobre la intersección de la hipotenusa AC con la mediatriz del segmento EJ, esto es, el punto N. Se sigue que N es punto medio del segmento AC. | ||
| − | De modo semejante, los triángulos EIB y JIB son triángulos rectángulos compartiendo la hipotenusa IB. Por lo tanto, los puntos E, I, J y B son concíclicos y el centro de la circunferencia que los contiene se halla sobre la intersección de la hipotenusa IB con la mediatriz del segmento EJ, esto es el punto F. De igual modo, se demuestra que los puntos M y P son los puntos medios de los lados BC y AB respectivamente. De forma análoga, se demuestra que los puntos D y H son puntos medios de los segmentos AI y CI respectivamente. | + | De modo semejante, los triángulos EIB y JIB son triángulos rectángulos compartiendo la hipotenusa IB. Por lo tanto, los puntos E, I, J y B son concíclicos y el centro de la circunferencia que los contiene se halla sobre la intersección de la hipotenusa IB con la mediatriz del segmento EJ, esto es el punto F. De igual modo, se demuestra que los puntos M y P son los puntos medios de los lados BC y AB respectivamente. De forma análoga, se demuestra que los puntos D y H son puntos medios de los segmentos AI y CI respectivamente. |
| − | == Circunferencias | + | == Circunferencias de Feuerbach y la circunscrita == |
Por la observación de que los puntos D, F y H satisfacen | Por la observación de que los puntos D, F y H satisfacen | ||
| − | :IA = 2ID; IB = IF; IC = 2IH | + | : IA = 2ID; IB = IF; IC = 2IH |
se deduce que: | se deduce que: | ||
| − | * la circunferencia de Feuerbach de un triángulo es [[homotecia|homotética]] a la [[ | + | * la circunferencia de Feuerbach de un triángulo es [[homotecia|homotética]] a la [[circuncentro|circunferencia circunscrita]], |
| − | * el centro de | + | * el centro de homotecia es el ortocentro del triángulo, |
* la razón de la homotecia es 2. | * la razón de la homotecia es 2. | ||
| − | El triángulo formado por los puntos D, F y H<ref> Estos puntos son los llamados | + | El triángulo formado por los puntos D, F y H<ref>Estos puntos son los llamados «puntos de Euler» y el triángulo determinado por ellos, el «triángulo de Euler».</ref> es semejante al triángulo ABC. También se observa que N (el centro de la circunferencia de Feuerbach) es el punto medio del segmento IO, donde O es el «circuncentro» del triángulo ABC. |
Finalmente, el centro de la circunferencia de Feuerbach se halla sobre la recta de Euler del triángulo. | Finalmente, el centro de la circunferencia de Feuerbach se halla sobre la recta de Euler del triángulo. | ||
== Aspectos diversos== | == Aspectos diversos== | ||
| − | |||
| − | La demostración de esta ocurrencia | + | En 1822, Karl Feuerbach descubrió una de las propiedades más profundas sobre la circunferencia que lleva su nombre: la circunferencia de los nueve puntos es tangente exterior a los círculos exinscritos al triángulo. La circunferencia inscrita al triángulo es tangente interior a la circunferencia de Feuerbach. |
| + | |||
| + | La demostración de esta ocurrencia puede hacerse, observando que los puntos de tangencia de dos de las circunferencias exinscritas a uno de los lados del triángulo equidistan del punto medio de dicho lado. Usando la inversión respecto de este punto medio se le puede dar el toque final a la demostración. | ||
| − | |||
| − | |||
== Fuentes == | == Fuentes == | ||
| − | * Donaire Peña, Milton (2010): ''Formas y números''. Lima (Perú): Ediciones UCH, 2010. | + | {{listaref}} |
| − | + | :* Donaire Peña, Milton (2010): ''Formas y números''. Lima (Perú): Ediciones UCH, 2010. | |
| − | * [https://es.wikipedia.org/wiki/Circunferencia_de_los_nueve_puntos Wikipedia | + | :* [https://es.wikipedia.org/wiki/Circunferencia_de_los_nueve_puntos «Circunferencia de los nueve puntos»], artículo publicado en el sitio web Wikipedia. |
| − | [[Categoría:Geometría]] | + | [[Categoría: Geometría]] |
| − | [[Categoría:Matemáticas | + | [[Categoría: Matemáticas]] |
| − | |||
Revisión del 13:27 8 oct 2019
| ||||||
La circunferencia de los nueve puntos, circunferencia de Feuerbach o circunferencia de Euler es la circunferencia que puede trazarse por puntos ligados a un triángulo escaleno no obtusángulo.
Se la conoce con varios nombres:
- circunferencia de Feuerbach, tal como conocen en el mundo alemán[1]
- circunferencia de Euler, en el ámbito francés
- circunferencia de los nueve puntos, en el área anglosajona, Latinoamérica, Rusia, Japón, India y China.
Su nombre, mencionando el cardinal de un conjunto de puntos, se debe a que la circunferencia atraviesa nueve puntos con nombre propio, seis de ellos sobre el mismo triángulo. Son los siguientes nueve puntos:
- Los tres centros de los tres lados del triángulo.
- Los tres pies de las alturas de tal triángulo.
- Los tres centros de cada uno de los segmentos que unen los tres vértices del triángulo con su ortocentro.
Sumario
Síntesis histórica
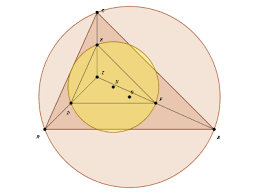
Tradicionalmente, se adjudica al alemán Karl Feuerbach (1800-1934) el hallazgo de la circunferencia de los nueve puntos; sin embargo, lo que él encontró fue la circunferencia de los seis puntos, reconociendo que sobre ella se encuentran los puntos medios de los lados de un triángulo y los pies de las alturas (en la figura, los puntos: M N P y E G J).
Anteriormente, Carlos Brianchon y Juan-Victor Fernandes habían demostrado su existencia. Poco tiempo después de Feuerbach, el francés Olry Terquem (1782-1862) también demostró la existencia del círculo y reconoció además que los puntos medios de los segmentos determinados por los vértices del triángulo y el ortocentro, además están ubicados en la circunferencia (en la figura, los puntos: D F H).
Denominación
Poncelet la llamó «circunferencia de los nueve puntos», nombre mayormente empleado en los países de habla inglesa. Algunos geómetras franceses la llaman «círculo de Euler» (o «circunferencia de Euler») y los geómetras teutones la denominan «circunferencia de Feuerbach», y en México, «circunferencia de los nueve puntos» (sic).[2]
Charles Wexler lo presenta como un teorema notable de geometría moderna e indica sus propiedades.[3] Pero en la obra de Levi Shively (1953),[4] en la primera edición en castellano, en Latinoamérica, ya se conocía con el nombre de la «circunfrencia de los nueve puntos».[5]
Proposición
Los puntos que bisecan los lados, los pies de las alturas también los puntos que bisecan los segmentos que conectan los vértices con el ortocentro de todo triángulo pertenecen a una misma circunferencia.[4]
Demostación
Consideremos las alturas del triángulo ABC: AE, BG y CJ (véase la figura). El triángulo GEJ es el triángulo «órtico» del triángulo ABC, y el punto I es el ortocentro del triángulo ABC. Las alturas de este, son las bisectrices de los ángulos internos de aquel. Los lados del triángulo ABC son las bisectrices exteriores del triángulo GEJ.
Las bisectrices del ángulo JGE cortan a la mediatriz del lado opuesto, EJ en los puntos F y N que se hallan sobre la circunferencia circunscrita c (descrito en el artículo de la bisectriz de un ángulo).
Observemos que los triángulos ACJ y ACE son triángulos rectángulos teniendo ambos al lado AC como hipotenusa. Se sigue que los cuatro puntos A, C, E y J son concíclicos y el centro de la circunferencia que los contiene se halla sobre la intersección de la hipotenusa AC con la mediatriz del segmento EJ, esto es, el punto N. Se sigue que N es punto medio del segmento AC.
De modo semejante, los triángulos EIB y JIB son triángulos rectángulos compartiendo la hipotenusa IB. Por lo tanto, los puntos E, I, J y B son concíclicos y el centro de la circunferencia que los contiene se halla sobre la intersección de la hipotenusa IB con la mediatriz del segmento EJ, esto es el punto F. De igual modo, se demuestra que los puntos M y P son los puntos medios de los lados BC y AB respectivamente. De forma análoga, se demuestra que los puntos D y H son puntos medios de los segmentos AI y CI respectivamente.
Circunferencias de Feuerbach y la circunscrita
Por la observación de que los puntos D, F y H satisfacen
- IA = 2ID; IB = IF; IC = 2IH
se deduce que:
- la circunferencia de Feuerbach de un triángulo es homotética a la circunferencia circunscrita,
- el centro de homotecia es el ortocentro del triángulo,
- la razón de la homotecia es 2.
El triángulo formado por los puntos D, F y H[6] es semejante al triángulo ABC. También se observa que N (el centro de la circunferencia de Feuerbach) es el punto medio del segmento IO, donde O es el «circuncentro» del triángulo ABC.
Finalmente, el centro de la circunferencia de Feuerbach se halla sobre la recta de Euler del triángulo.
Aspectos diversos
En 1822, Karl Feuerbach descubrió una de las propiedades más profundas sobre la circunferencia que lleva su nombre: la circunferencia de los nueve puntos es tangente exterior a los círculos exinscritos al triángulo. La circunferencia inscrita al triángulo es tangente interior a la circunferencia de Feuerbach.
La demostración de esta ocurrencia puede hacerse, observando que los puntos de tangencia de dos de las circunferencias exinscritas a uno de los lados del triángulo equidistan del punto medio de dicho lado. Usando la inversión respecto de este punto medio se le puede dar el toque final a la demostración.
Fuentes
- ↑ Donaire Peña, Milton: Formas y números.
- ↑ Eves, Howard (1969): Estudio de las geometrías I (pág. 126). México: Uteha, 1969. ISBN 968-438-780-6.
- ↑ Wexler, Charles (1977): Geometría analítica. Un enfoque vectorial (pág. 104). Barcelona (Cataluña): Montaner y Simon, 1977. ISBN 84-274-0394-1.
- ↑ 4,0 4,1 Shively, Levi S. (1953): Introducción a la geometría moderna.
- ↑ La primera edición en castellano de Howard Eves data en 1969; podría ser una llevada de agua para su molino de parte de los traductores.
- ↑ Estos puntos son los llamados «puntos de Euler» y el triángulo determinado por ellos, el «triángulo de Euler».
- Donaire Peña, Milton (2010): Formas y números. Lima (Perú): Ediciones UCH, 2010.
- «Circunferencia de los nueve puntos», artículo publicado en el sitio web Wikipedia.