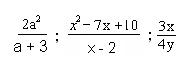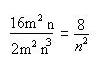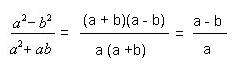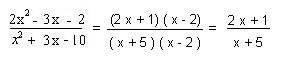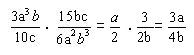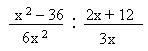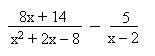Diferencia entre revisiones de «Fracción algebraica»
| Línea 31: | Línea 31: | ||
[[Image:Resuelto 1a).JPG]]<br> | [[Image:Resuelto 1a).JPG]]<br> | ||
| − | + | [[Image:Ej 1 b).JPG]]<br> | |
Aquí no se puede simplificar directamente; tenemos que descomponer en factores el numerador y el denominador <br> | Aquí no se puede simplificar directamente; tenemos que descomponer en factores el numerador y el denominador <br> | ||
[[Image:Resuelto 1b).JPG]]<br> | [[Image:Resuelto 1b).JPG]]<br> | ||
| − | + | [[Image:Ej 1 c).JPG]]<br> | |
Factorizando ambos trinomios: <br> | Factorizando ambos trinomios: <br> | ||
| Línea 51: | Línea 51: | ||
Ejemplo: <br> | Ejemplo: <br> | ||
Efectúa las multiplicaciones siguientes:<br> | Efectúa las multiplicaciones siguientes:<br> | ||
| − | + | [[Image:Mutiplic a).JPG]]<br> | |
| − | |||
Como los denominadores y los numeradores son monomios, se procede a simplificar y después efectuamos los productos indicados.<br> | Como los denominadores y los numeradores son monomios, se procede a simplificar y después efectuamos los productos indicados.<br> | ||
| − | |||
[[Image:Resuelto Mutiplic a).JPG]]<br> | [[Image:Resuelto Mutiplic a).JPG]]<br> | ||
| − | + | [[Image: Multiplic b).JPG]]<br> | |
| − | |||
| − | |||
Descomponemos en este caso el numerador del primer factor (diferencia de cuadrado), el numerador del segundo factor (binomio, extracción de factor común) y el denominador del segundo factor (trinomio)<br> | Descomponemos en este caso el numerador del primer factor (diferencia de cuadrado), el numerador del segundo factor (binomio, extracción de factor común) y el denominador del segundo factor (trinomio)<br> | ||
Simplificamos y efectuamos la multiplicación | Simplificamos y efectuamos la multiplicación | ||
| Línea 65: | Línea 61: | ||
===División=== | ===División=== | ||
El procedimiento para dividir fracciones algebraicas es el mismo que ya conoces para dividir fracciones comunes. | El procedimiento para dividir fracciones algebraicas es el mismo que ya conoces para dividir fracciones comunes. | ||
| − | + | Si tenemos las fracciones algebraicas[[Image:Expres Algeb.JPG]]se cumple que:<br> | |
[[Image:DivisiónJPG]]<br> | [[Image:DivisiónJPG]]<br> | ||
Luego:<br> | Luego:<br> | ||
| Línea 71: | Línea 67: | ||
Ejemplo:<br> | Ejemplo:<br> | ||
Efectúa las divisiones siguientes<br> | Efectúa las divisiones siguientes<br> | ||
| − | + | [[Image:División a).JPG]]<br> | |
| − | |||
#Efectuamos el producto del dividendo por el recíproco del divisor. | #Efectuamos el producto del dividendo por el recíproco del divisor. | ||
#Descomponemos: en el numerador del primer factor la diferencia de cuadrado y extraemos factor común en el denominador del segundo factor. | #Descomponemos: en el numerador del primer factor la diferencia de cuadrado y extraemos factor común en el denominador del segundo factor. | ||
#Efectuamos la multiplicación y eliminamos el paréntesis. | #Efectuamos la multiplicación y eliminamos el paréntesis. | ||
[[Image: Resuelto División a).JPG]] <br> | [[Image: Resuelto División a).JPG]] <br> | ||
| − | + | [[Image: División b.JPG]] <br> | |
| − | [[Image:Resuelto División b) .JPG]] <br> | + | [[Image:Resuelto División b).JPG]] <br> |
===Adición y sustracción=== | ===Adición y sustracción=== | ||
Para adicionar o sustraer fracciones algebraicas se procede de forma análoga que para multiplicar fracciones comunes. | Para adicionar o sustraer fracciones algebraicas se procede de forma análoga que para multiplicar fracciones comunes. | ||
| Línea 88: | Línea 83: | ||
Ejemplo.<br> | Ejemplo.<br> | ||
Calcula y simplifica si es posible.<br> | Calcula y simplifica si es posible.<br> | ||
| − | + | [[Image: Adic y sust a).JPG]] | |
*Se determina el m.c.m de 6a y 4a<sup>2</sup>, que es 12a<sup>2</sup>. | *Se determina el m.c.m de 6a y 4a<sup>2</sup>, que es 12a<sup>2</sup>. | ||
*Se divide este término por 6a y 4a<sup>2</sup> respectivamente y se obtiene los factores de ampliación 2a y 3. | *Se divide este término por 6a y 4a<sup>2</sup> respectivamente y se obtiene los factores de ampliación 2a y 3. | ||
| Línea 94: | Línea 89: | ||
*Se efectúan los productos indicados y se agrupan términos semejantes. | *Se efectúan los productos indicados y se agrupan términos semejantes. | ||
*Se simplifica si es posible | *Se simplifica si es posible | ||
| − | |||
[[Image: Resuelto Adic y sust a).JPG]] | [[Image: Resuelto Adic y sust a).JPG]] | ||
| − | + | [[Image: Adic y sust b).JPG]] | |
*Para determinar el m.c.m se factoriza el denominador de la primera fracción, luego el m.c.m es (x + 4) (x – 2), ya que dicha expresión contiene a (x – 2) | *Para determinar el m.c.m se factoriza el denominador de la primera fracción, luego el m.c.m es (x + 4) (x – 2), ya que dicha expresión contiene a (x – 2) | ||
*Se divide el m.c.m por cada denominador y se amplían los numeradores. | *Se divide el m.c.m por cada denominador y se amplían los numeradores. | ||
| Línea 102: | Línea 96: | ||
*Se agrupan términos semejante y se simplifica si es posible. | *Se agrupan términos semejante y se simplifica si es posible. | ||
[[Image: Resuelto Adic y sust b).JPG]] | [[Image: Resuelto Adic y sust b).JPG]] | ||
| − | == Véase también | + | == Véase también == |
*[[Expresiones Algebraicas|Expresiones Algebraicas]] | *[[Expresiones Algebraicas|Expresiones Algebraicas]] | ||
| − | == | + | == Fuentes == |
*Libro de texto de Matemática 9no Grado. | *Libro de texto de Matemática 9no Grado. | ||
| − | * | + | *[http://www.vitutor.com Vitutor] |
| − | * | + | *[http://www.geolay.com Álgebra] |
[[Category:Álgebra]] | [[Category:Álgebra]] | ||
Revisión del 17:38 26 may 2011
| ||||||
Fracciones Algebraicas: Cociente de dos polinomios. Estas se pueden representar de la siguiente forma:
Sumario
Fracciones algebraicas
Si A y B son dos expresiones algebraicas con B ≠ 0, y en B aparece al menos una variable con exponente entero positivo, el cociente indicado recibe el nombre de fracción algebraica.
Son fracciones algebraicas:
Simplificación y ampliación de fracciones algebraicas
En una fracción algebraica, al igual que una fracción numérica, también es posible multiplicar o dividir el numerador y el denominador por un mismo factor (diferente de cero), obteniéndose así una nueva fracción equivalente a la fracción dada.
Para amplificar una fracción algebraica se multiplica el numerador y el denominador de la fracción por un polinomio.
Ejemplo:
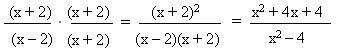
Ejemplo:
Simplifica las fracciones algebraicas siguientes:
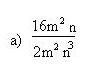
Para simplificar esta expresión algebraica dividimos el numerador y el denominador por 2m2n (que es el mayor factor común a ambos).
Aquí no se puede simplificar directamente; tenemos que descomponer en factores el numerador y el denominador
Operaciones con fracciones algebraicas
Multiplicación
Para multiplicar fracciones algebraicas se procede de forma análoga que para multiplicar fracciones comunes.
Si tenemos las fracciones algebraicas se cumple que:
Con el objetivo de obtener un resultado ya simplificado, es conveniente proceder de la forma siguiente:
- Factorizar los numeradores y denominadores de las fracciones dadas (cuando no lo estén ya).
- Simplificar los factores que se comunes a los numeradores y denominadores.
- Efectuar las multiplicaciones indicadas.
Ejemplo:
Efectúa las multiplicaciones siguientes:
Como los denominadores y los numeradores son monomios, se procede a simplificar y después efectuamos los productos indicados.
Descomponemos en este caso el numerador del primer factor (diferencia de cuadrado), el numerador del segundo factor (binomio, extracción de factor común) y el denominador del segundo factor (trinomio)
Simplificamos y efectuamos la multiplicación
Eliminamos el paréntesis multiplicando 2 por m+2
División
El procedimiento para dividir fracciones algebraicas es el mismo que ya conoces para dividir fracciones comunes.
Si tenemos las fracciones algebraicasse cumple que:
Archivo:DivisiónJPG
Luego:
Para dividir una fracción algebraica por otra, se efectúa el producto del dividendo por el recíproco del divisor.
Ejemplo:
Efectúa las divisiones siguientes
- Efectuamos el producto del dividendo por el recíproco del divisor.
- Descomponemos: en el numerador del primer factor la diferencia de cuadrado y extraemos factor común en el denominador del segundo factor.
- Efectuamos la multiplicación y eliminamos el paréntesis.
Archivo:Resuelto División a).JPG
Archivo:División b.JPG
Archivo:Resuelto División b).JPG
Adición y sustracción
Para adicionar o sustraer fracciones algebraicas se procede de forma análoga que para multiplicar fracciones comunes.
Luego aplicaremos el procedimiento siguiente:
- Determinar el m.c.m de los denominadores, que será el denominador común.
- Dividir el denominador común por cada uno de los denominadores y ampliar los numeradores
- Efectuar los productos indicados en el numerador y reducir términos semejantes, en caso de que existan.
- Simplificar el resultado si es posible.
Ejemplo.
Calcula y simplifica si es posible.
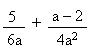
- Se determina el m.c.m de 6a y 4a2, que es 12a2.
- Se divide este término por 6a y 4a2 respectivamente y se obtiene los factores de ampliación 2a y 3.
- Se multiplica 2a por 5 y 3 por a – 2
- Se efectúan los productos indicados y se agrupan términos semejantes.
- Se simplifica si es posible
- Para determinar el m.c.m se factoriza el denominador de la primera fracción, luego el m.c.m es (x + 4) (x – 2), ya que dicha expresión contiene a (x – 2)
- Se divide el m.c.m por cada denominador y se amplían los numeradores.
- Se efectúan los productos indicados.
- Se agrupan términos semejante y se simplifica si es posible.