Diferencia entre revisiones de «Ley de Faraday»
| Línea 1: | Línea 1: | ||
| − | |||
{{Definición | {{Definición | ||
| − | |nombre=Ley | + | |nombre=Ley de Faraday |
|imagen=leyfaraday.jpg | |imagen=leyfaraday.jpg | ||
|tamaño= | |tamaño= | ||
| − | |concepto=El [[voltaje | + | |concepto=El [[Voltaje|voltaje]] inducido en un [[Circuito|circuito]] cerrado es directamente proporcional a la rapidez con que cambia en el tiempo el flujo magnético que atraviesa una superficie cualquiera con el circuito como borde |
| − | }} | + | }} |
| + | '''Ley de Faraday'''. Se basa en los experimentos realizados por [[Michael Faraday]] en [[Inglaterra]] en [[1831]] y por [[Joseph Henry]] en [[Estados Unidos]] casi al mismo tiempo. Faraday publicó sus resultados primero, lo cual le da la prioridad del descubrimiento. | ||
| − | == La ley de | + | == La ley de inducción de Faraday == |
| − | + | Imaginar que existen dos líneas de un [[campo magnético]] proveniente de un [[Imán|imán]] y de una espira de corriente que algunas de esas líneas del campo pasan a través de una bobina, cuando se mueve el imán o se abre o se cierra el interruptor el número de líneas del campo magnético que pasan a través de la bobina cambia. Como lo demostraron los experimentos de Faraday, y como la técnica de Faraday de las líneas de campo nos ayuda a percibir, lo que induce la fem en el anillo es el cambio en el número de líneas de campo que pasan a través de un circuito cerrado. Específicamente, lo que determina la fem inducida es la velocidad de cambio en el número de líneas de campo que pasan a través del anillo, por lo que establece que el [[Voltaje|voltaje]] inducido en un [[Circuito|circuito]] cerrado es directamente proporcional a la rapidez con que cambia en el tiempo el flujo magnético que atraviesa una superficie cualquiera con el circuito como borde: | |
[[Image:Ecuacion1.png|left|Ecuacion1.png]]<br> | [[Image:Ecuacion1.png|left|Ecuacion1.png]]<br> | ||
| Línea 17: | Línea 17: | ||
<br> | <br> | ||
| − | Donde '''E''' es el campo eléctrico, '''dl''' es el elemento infinitesimal del contorno C, '''B''' es la [[Densidad de campo magnético | + | Donde '''E''' es el campo eléctrico, '''dl''' es el elemento infinitesimal del contorno C, '''B''' es la [[Densidad|densidad]] de campo magnético y S es una superficie arbitraria, cuyo borde es C. Las direcciones del contorno C y de '''dA''' están dadas por la Regla de la mano derecha. |
La permutación de la integral de superficie y la derivada temporal se puede hacer siempre y cuando la superficie de integración no cambie con el tiempo. | La permutación de la integral de superficie y la derivada temporal se puede hacer siempre y cuando la superficie de integración no cambie con el tiempo. | ||
| Línea 29: | Línea 29: | ||
<br> | <br> | ||
| − | + | Esta es una de las [[Ecuaciones de Maxwell]], las cuales conforman las ecuaciones fundamentales del [[Electromagnetismo]]. La ley de Faraday, junto con las otras leyes del Electromagnetismo, fue incorporada en las ecuaciones de Maxwell, unificando así al electromagnetismo. En el caso de un [[Inductor|inductor]] con N vueltas de alambre, la fórmula anterior se transforma en: | |
'''Vε = -N (dΦ/dt)''' | '''Vε = -N (dΦ/dt)''' | ||
| − | donde '''Vε''' es el [[Voltaje | + | donde '''Vε''' es el [[Voltaje|voltaje]] inducido y '''dΦ/dt''' es la tasa de variación temporal del flujo magnético '''Φ'''. La dirección voltaje inducido (el signo negativo en la fórmula) se debe a la [[Ley de Lenz]]. |
== Consideraciones == | == Consideraciones == | ||
| Línea 46: | Línea 46: | ||
== Fuente == | == Fuente == | ||
| − | * | + | *Halliday, D.[[ Física]] Volumen 2.Versión Ampliada, Cuarta Edición [[1992]]. ISBN 0-08-021680-3<br> |
| − | |||
[[Category:Física]] | [[Category:Física]] | ||
Revisión del 12:29 8 jun 2011
| ||||||
Ley de Faraday. Se basa en los experimentos realizados por Michael Faraday en Inglaterra en 1831 y por Joseph Henry en Estados Unidos casi al mismo tiempo. Faraday publicó sus resultados primero, lo cual le da la prioridad del descubrimiento.
La ley de inducción de Faraday
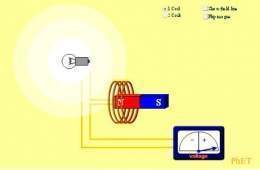
Imaginar que existen dos líneas de un campo magnético proveniente de un imán y de una espira de corriente que algunas de esas líneas del campo pasan a través de una bobina, cuando se mueve el imán o se abre o se cierra el interruptor el número de líneas del campo magnético que pasan a través de la bobina cambia. Como lo demostraron los experimentos de Faraday, y como la técnica de Faraday de las líneas de campo nos ayuda a percibir, lo que induce la fem en el anillo es el cambio en el número de líneas de campo que pasan a través de un circuito cerrado. Específicamente, lo que determina la fem inducida es la velocidad de cambio en el número de líneas de campo que pasan a través del anillo, por lo que establece que el voltaje inducido en un circuito cerrado es directamente proporcional a la rapidez con que cambia en el tiempo el flujo magnético que atraviesa una superficie cualquiera con el circuito como borde:
Donde E es el campo eléctrico, dl es el elemento infinitesimal del contorno C, B es la densidad de campo magnético y S es una superficie arbitraria, cuyo borde es C. Las direcciones del contorno C y de dA están dadas por la Regla de la mano derecha.
La permutación de la integral de superficie y la derivada temporal se puede hacer siempre y cuando la superficie de integración no cambie con el tiempo.
Por medio del Teorema de Stokes puede obtenerse una forma diferencial de esta ley:
Esta es una de las Ecuaciones de Maxwell, las cuales conforman las ecuaciones fundamentales del Electromagnetismo. La ley de Faraday, junto con las otras leyes del Electromagnetismo, fue incorporada en las ecuaciones de Maxwell, unificando así al electromagnetismo. En el caso de un inductor con N vueltas de alambre, la fórmula anterior se transforma en:
Vε = -N (dΦ/dt)
donde Vε es el voltaje inducido y dΦ/dt es la tasa de variación temporal del flujo magnético Φ. La dirección voltaje inducido (el signo negativo en la fórmula) se debe a la Ley de Lenz.
Consideraciones
Es preciso observar, que aun cuando la ecuación se conoce como la ley de Faraday, no fue escrita en esa forma por Faraday, quien carecía de una formación Matemática. De hecho, la obra en tres volúmenes que publicó Faraday sobre Magnetismo, y que constituye un hito en el desarrollo de Física y de la Química no contiene una sola ecuación