Geometría fractal
| ||||
Geometría fractal es una rama de la geometría que estudia estructuras matemáticas que se asemejan a patrones naturales, integrando lo matemático y lo visual en un paradigma que redefine nuestra percepción de lo real. Este enfoque combina objetos matemáticos con estructuras naturales, ofreciendo un modelo que inaugura una nueva visión de lo existente.
Los fractales son objetos semi-geométricos (por su irregularidad no pertenecen a la geometría tradicional) cuya estructura básica se repite a diferentes escalas. Los fractales pueden ser creados por el hombre con intenciones artísticas o encontrarse naturalmente en estructuras como copos de nieve.
Sumario
Origen e historia
El matemático francés Benoît Mandelbrot desarrolló en 1975 el concepto de fractal, término derivado del latín fractus (“quebrado”). Desde entonces, los fractales han sido aceptados por la comunidad científica e incluso forman parte del diccionario de la Real Academia Española.
Antes de los años 70, la matemática fractal se consideraba una curiosidad y permanecía relegada a los márgenes. En 1919, Hausdorff ideó un método para medir dimensiones y medidas de fractales, denominado medida y dimensión Hausdorff. Un año después, Besicovitch expandió este trabajo creando la teoría geométrica de la medida.
En 1963, Edward Lorenz, meteorólogo, descubrió el efecto mariposa al redondear decimales en un programa de simulación meteorológica. Variaciones mínimas en las condiciones iniciales resultaron en resultados impredecibles, marcando el nacimiento del caos matemático.
Efecto mariposa: El aleteo de una mariposa en un lugar remoto puede desencadenar un tornado en otro. Esto muestra cómo pequeñas variaciones iniciales producen cambios impredecibles en sistemas dinámicos.
Gastón Julia (1893–1978) exploró las iteraciones de funciones complejas y publicó el artículo “Informe sobre la iteración de las funciones racionales” en la revista francesa Journal de Mathématiques Pures et Appliquées. Allí introdujo el conjunto de Julia.
Mandelbrot publicó The Fractal Geometry of Nature (1977, 1982, 1983), estableciendo las bases de la geometría fractal. En 1987, Michael F. Barnsley introdujo la transformación fractal, permitiendo la compresión de imágenes digitales.
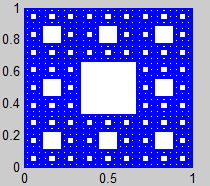
Autosimilitud de los fractales
Según Mandelbrot, los fractales pueden presentar tres tipos de autosimilitud:
- Autosimilitud exacta: El fractal resulta idéntico en cualquier escala.
- Cuasiautosimilitud: Con el cambio de escala, las copias del conjunto son semejantes, pero no idénticas.
- Autosimilitud estadística: El fractal conserva medidas numéricas o estadísticas con el cambio de escala.
Uso de los fractales
Compresión de imágenes
Las técnicas fractales se utilizan para la compresión de datos. Gracias al teorema del collage, es posible encontrar un IFS (sistema de funciones iteradas) que codifique la información de una figura completa en cada una de sus partes autosemejantes.
Efectos visuales
Los fractales son usados comercialmente en la industria cinematográfica, como en películas como Star Wars y Star Trek, para generar paisajes fabulosos sin necesidad de sets costosos.
Música fractal
Ciertas músicas, como las de Bach y Mozart, retienen su esencia incluso al ser reducidas. Se han desarrollado softwares para crear música fractal.
Modelado de formas naturales
Las formas fractales son comunes en la biología y permiten el desarrollo de estructuras complejas, como hojas, ramas y árboles, que muestran similitudes entre sus partes y el todo.
Sistemas dinámicos
Los fractales también aparecen en la dinámica evolutiva de sistemas complejos, reflejando ciclos de desarrollo que producen nuevas realidades más sofisticadas.
Fractal autosemejante
Son los atractores de un sistema de funciones iteradas contractivo.
Ejemplos
Pentágono de Sierpinski:
Alfombra de Sierpinski:
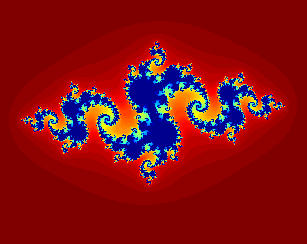
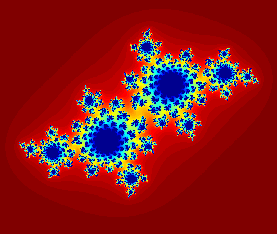
Conjunto de Mandelbrot
El conjunto de Mandelbrot incluye los puntos del plano complejo para los cuales la "sucesión de Mandelbrot" está acotada en módulo.
Ejemplos
Sucesión zn+1 = zn4+c:
Sucesión zn+1 = zn-3+c:
Conjunto de Julia lleno
El conjunto de Julia lleno de la función f contiene los puntos del plano complejo cuyas iteraciones no divergen.