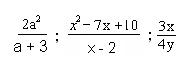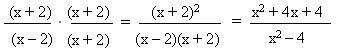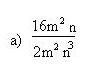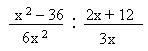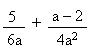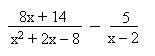Fracción algebraica

Fracción algebraica 260px Concepto: Fraccion que tienen una variable en el denominador

Fracción algebraica. Es el cociente de dos polinomios.

Fracciones algebraicas

Si A y B son dos expresiones algebraicas con B ≠ 0, y en B aparece al menos una variable con exponente entero positivo, el cociente indicado recibe el nombre de fracción algebraica.

Fracciones algebraicas

Si A y B son dos expresiones algebraicas con B ≠ 0, y en B aparece al menos una variable con exponente entero positivo, el cociente indicado recibe el nombre de fracción algebraica.

Por ejemplo:

Simplificación y ampliación de fracciones algebraicas

En una fracción algebraica, al igual que una fracción numérica, también es posible multiplicar o dividir el numerador y el denominador por un mismo factor (diferente de cero), obteniéndose así una nueva fracción equivalente a la fracción dada.

Para amplificar una fracción algebraica se multiplica el numerador y el denominador de la fracción por un polinomio. Ejemplo:

Para simplificar esta expresión algebraica dividimos el numerador y el denominador por 2m2n (que es el mayor factor común a ambos). Ejemplo:

Simplifica las fracciones algebraicas siguientes:

Archivo:Resuelto a).JPG b) Archivo:Imagen: Ej 1 b).JPG

Aquí no se puede simplificar directamente; tenemos que descomponer en factores el numerador y el denominador Archivo:Resuelto b).JPG c)

Factorizando ambos trinomios:

Archivo:Resuelto c).JPG

Operaciones con fracciones

Multiplicación

Para multiplicar fracciones algebraicas se procede de forma análoga que para multiplicar fracciones comunes. Si tenemos las fracciones algebraicas se cumple que. Con el objetivo de obtener un resultado ya simplificado, es conveniente proceder de la forma siguiente: Factorizar los numeradores y denominadores de las fracciones dadas (cuando no lo estén ya). Simplificar los factores que se comunes a los numeradores y denominadores. Efectuar las multiplicaciones indicadas. Ejemplo: Efectúa las multiplicaciones siguientes: a) Archivo:Multiplic a).JPG

Como los denominadores y los numeradores son monomios, se procede a simplificar y después efectuamos los productos indicados.

Archivo:Resuelto Multiplic a).JPG 

b)

Descomponemos en este caso el numerador del primer factor (diferencia de cuadrado), el numerador del segundo factor (binomio, extracción de factor común) y el denominador del segundo factor (trinomio) Simplificamos y efectuamos la multiplicación Eliminamos el paréntesis multiplicando 2 por m+2

División

El procedimiento para dividir fracciones algebraicas es el mismo que ya conoces para dividir fracciones comunes.

Si tenemos las fracciones algebraicas se cumple que.

Archivo:DivisiónJPG

Luego: Para dividir una fracción algebraica por otra, se divide el producto del dividendo por el recíproco del divisor. Ejemplo. Efectúa las divisiones siguientes

Efectuamos el producto del dividendo por el recíproco del divisor. Descomponemos: en el numerador del primer factor la diferencia de cuadrado y extraemos factor común en el denominador del segundo factor. Efectuamos la multiplicación y eliminamos el paréntesis.

Archivo:Resuelto División a).JPG

b)

Archivo:División b).JPG

Archivo:Resuelto División b) .JPG

===Adición y sustracción de fracciones algebraicas===.

Para adicionar o sustraer fracciones algebraicas se procede de forma análoga que para multiplicar fracciones comunes.

Luego aplicaremos el procedimiento siguiente: Determinar el m.c.m de los denominadores, que será el denominador común. Dividir el denominador común por cada uno de los denominadores y ampliar los numeradores Efectuar los productos indicados en el numerador y reducir términos semejantes, en caso de que existan. Simplificar el resultado si es posible. Ejemplo. Calcula y simplifica si es posible. a)

• Se determina el m.c.m de 6a y 4a2, que es 12 a2.
• Se divide este término por 6a y 4 a2 respectivamente y se obtiene los factores de ampliación 2a y 3.
• Se multiplica 2a por 5 y 3 por a – 2
• Se efectúan los productos indicados y se agrupan términos semejantes.
• Se simplifica si es posible

b)

• Para determinar el m.c.m se factoriza el denominador de la primera fracción, luego el m.c.m es (x + 4) (x – 2), ya que dicha expresión contiene a x – 2
• Se divide el m.c.m por cada denominador y se amplían los numeradores.
• Se efectúan los productos indicados.
• Se agrupan términos semejante y se simplifica si es posible.

Véase también.

• Expresiones Algebraicas

Fuente

• Libro de texto de Matemática 9no Grado.