Estrofoide
Revisión del 08:32 8 ago 2011 de CiroRedondo1 jc (discusión | contribuciones) (Página creada con '{{Desarrollo}} {{Definición |nombre=Estrofoide |imagen=Estrofoide.png |tamaño= |concepto= }} <div align="justify"> '''Estrofoide'''. Es el lugar geométrico de los puntos ...')
| ||||
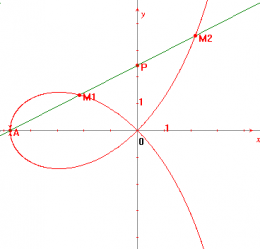
Estrofoide. Es el lugar geométrico de los puntos M1 y M2. (que yacen en rayos arbitrarios que pasan por el punto A), para los cuales PM1=PM2=OP (P es un punto arbitrario del eje Oy).
Definición
Es el lugar geométrico de los puntos que satisfacen la ecuación implícita:
La ecuación implícita anterior , tiene como ecuaciones paramétricas a:
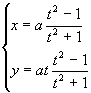donde el parámetro t es la tangente del triángulo BOx.
En coordenadas polares es: Archivo:Coordpolares estrofoide.gif
Propiedades
- Es una curva abierta, consiste en dos arcos de curva (ramas) sin puntos comunes que se prolongan ilimitadamente.
- Tiene dos ejes de simetría perpendiculares; por tanto es centralmente simétrica y tiene un centro.
- Un eje de simetría no contiene puntos de la curva
Aplicaciones
Fuentes
- Dr. Brigitte, Frank y otros. Matemática 12 Libro de texto para el 12 grado, La habana, 1983.
- Datos de una parábola
