Lemniscata de Bernoulli
| ||||
Lemniscata de Bernoulli. En matemática, una lemniscata es un tipo de curva descrita por la siguiente ecuación en coordenadas cartesianas:
Historia
La Lemniscata se considera actualmente como un caso particular de los óvalos estudiados por Jean Dominique Cassini en 1680, pero son Jackob Bernoulli y Johann Bernoulli los que la descubrieron y dieron a conocer independientemente, al intentar resolver un problema planteado por Leibnitz creador, junto con Isaac Newton del cálculo infinitesimal, que lanzó a la comunidad científica de la época el reto de encontrar la ecuación de la isócrona paracéntrica. La solución encontrada fue la Lemniscata que en honor a los hermanos Bernoulli paso a denominarse Lemniscata de Bernoulli.
Bernoulli la llamó lemniscus, que en Latín significa "cinta colgante".
La representación gráfica de esta ecuación genera una curva similar a ∞. La curva se ha convertido en el símbolo del infinito y es ampliamente utilizada en matemática.
Definición
Ecuaciones
- Ecuación en coordenadas cartesianas:
- La ecuación implícita anterior , tiene como ecuaciones paramétricas a:
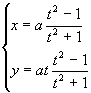, donde el parámetro t es la tangente del triángulo BOx.
- La lemniscata puede ser descrita mediante coordenadas polares según la siguiente ecuación:
r2=a2cos2θ
- Análogamente, con coordenadas bipolares su ecuación es:
rrʼ=a2/2
Construcción
Sea P un punto cualquiera de la circunferencia y Q el punto de intersección entre la semirrecta OP y la circunferencia. Se traza la circunferencia de centro O y radio PQ.
Sea M el punto de intersección de la semirrecta y la circunferencia de centro O.
El lugar geométrico descrito por el punto M y el simétrico de M respecto a O (M’), a medida que P se mueve en la circunferencia de centro F’, es una Lemniscata de Bernuolli.
Vea también
Fuentes
- Lemniscata [citado 2011 agosto, 18]; Disponible en:http:http://es.wikipedia.org/wiki/Lemniscata.
- [Ecuaciones Estrofoide[citado 2011 agosto, 18]; Disponible en:http://prepa8.unam.mx/colegios/mate/geogebra/parametricas_i.html ]
