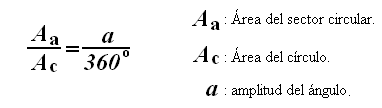Sector circular
| ||||||
Sector circular. Existen diferentes figuras geométricas como el cuadrado, el rectángulo, el trapecio, el círculo, la circunferencia, etcétera. Cada una ellas tienen sus definiciones y elementos y se les puede calcular el área, perímetro y la longitud.
Hace mucho tiempo los hombres se esforzaron por realizar estos cálculos por la importancia que tenían distintos objetos, principalmente circulares, empleados en la práctica. De ahí comenzó el estudio de los diferentes elementos que los componen, entre ellos el sector circular.
Sumario
Aplicaciones
Conociendo acerca del sector circular se puede calcular el área recorrida por un columpio al mecerse.
Asimismo se puede calcular el área que recorre el péndulo del reloj de pared. La cantidad de metros cuadrados que abarca un huerto con esta forma geométrica y con ella la cantidad de materiales que se emplearán para cercar sus límites.
Área de un sector circular
Se puede obtener una relación para calcular el área de un sector circular como se muestra a continuación.
Ejemplo
Calcula el área de un sector circular que tiene 20° de amplitud en un círculo de 2m de radio.
Perímetro de un sector circular
El perímetro es la suma de la longitud de sus lados, en este caso tiene dos lados iguales que es el radio del círculo y un arco, por tanto es necesario hallar la longitud del arco primeramente.
Longitud del arco
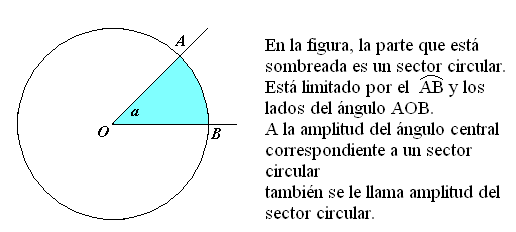
Para calcular la longitud de un arco de circunferencia se debe establecer una proporción donde L es la longitud de la circunferencia, b es la longitud del arco, a es la amplitud del ángulo central correspondiente y 360º es la amplitud total de la circunferencia. Quedando dicha proporción como se muestra a continuación:
Ejemplo
De una circunferencia de 4 cm de radio, calcula la longitud de un arco que tiene 30º de amplitud.
Si ya se conoce la longitud del arco correspondiente al sector circular y el radio de la circunferencia a la cual pertenece este, se puede calcular su perímetro de la siguiente forma:
Fuente
- Libro de texto de Matemática 8vo grado. Editorial Pueblo y Educación, 1990.