Diferencia entre revisiones de «Cuadrilátero»
(Página creada con '{{Definición|Nombre=Cuadrilátero|imagen=Cuadrilátero.JPG|concepto=Polígono de cuatro lados}}'''Rectángulo(Figura). ''' Los cuadriláteros son los polígonos que tienen cuat…') (Etiqueta: nuestro-nuestra) |
(Etiqueta: nuestro-nuestra) |
||
| Línea 1: | Línea 1: | ||
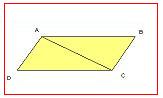
| − | {{Definición|Nombre=Cuadrilátero|imagen=Cuadrilátero.JPG|concepto=Polígono de cuatro lados}}''' | + | {{Definición|Nombre=Cuadrilátero|imagen=Cuadrilátero.JPG|concepto=Polígono de cuatro lados}}'''Cuadrilátero(Figura). ''' Los cuadriláteros son los [[Polígono|polígonos]] que tienen cuatro lados. Si te fijas, cerca de ti hay muchos objetos cuya línea de contorno tiene forma de cuadrilátero: una ventana, la pantalla de un ordenador o de un televisor plano, un póster, una puerta o el trapecio que forma en el suelo la luz del Sol que entra por la ventana. Los cuadriláteros son los polígonos que más abundan a nuestro alrededor, más que los [[Triángulo|triángulos ]]y, por supuesto, que los [[Pentágono|pentágonos]], [[Hexágono|hexágonos]], etc'''.''' |
| − | Los cuadriláteros son los polígonos que más abundan a nuestro alrededor, más que los triángulos y, por supuesto, que los pentágonos, | ||
| − | == | + | == Clasificación == |
| − | |||
| − | |||
| − | |||
| − | <br> | + | Los cuadriláteros de forma general se clasifican en dos grandes grupos: |
| + | |||
| + | |||
| + | |||
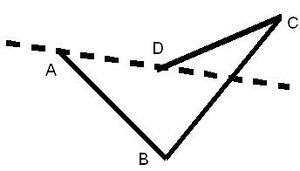
| + | *'''vos''': Son aquellos cuadriláteros, que al menos uno de sus lados cumple la condición de que la línea que lo contiene, divide a la figura en dos partes, o sea, la deja en ambos semiplanos en que divide la línea al plano. <br> | ||
| + | *'''''Convexos''''': Son aquellos cuadriláteros que cumplen la condición de que al prolongar cualquiera de sus lados, la línea que lo contiene deja al cuadrilátero en un solo semiplano. <br> | ||
| + | *<br> | ||
{| width="470" cellspacing="1" cellpadding="1" border="0" align="center" style="" | {| width="470" cellspacing="1" cellpadding="1" border="0" align="center" style="" | ||
|- | |- | ||
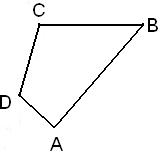
| − | | [[Image: | + | | [[Image:Cuadrilátero_cóncavo1.JPG|thumb|center|Cuadrilátero cóncavo]]<br> |
| − | | [[Image: | + | | [[Image:Cuadrilátero_convexo.JPG|thumb|center|204x129px|Cuadrilátero convexo]]<br> |
|} | |} | ||
<br> | <br> | ||
| − | == | + | == Tipos == |
| − | + | Los cuadriláteros se dividen en Paralelogramo, trapecios y Trapezoides.<br>'''''Paralelogramos''''': Tienen sus dos pares de lados opuestos paralelos.<br><br> | |
| − | [[Image: | + | [[Image:Paralelogramos.JPG|thumb|center|312x136px|Tipos de paralelogramos]]<br> |
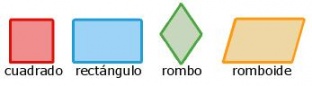
| − | + | *El [[Cuadrado|'''cuadrado''']]tiene los cuatro lados iguales y los cuatro ángulos rectos (90°). | |
| + | *El [[Rectángulo|'''rectángulo''']]tiene los lados iguales dos a dos y los cuatro ángulos rectos (90°). | ||
| + | *El [[Rombo|'''rombo''']]tiene los cuatro lados iguales, pero sus ángulos no miden 90°. | ||
| + | *El [[Romboide|'''romboide''']]tiene los lados iguales dos a dos, pero sus ángulos no miden 90°. <br><br> | ||
| − | + | '''''Trapecios''''': Tienen un solo par de lados paralelos.<br> | |
| − | [[Image: | + | {| cellspacing="1" cellpadding="1" border="0" align="center" style="width: 622px; height: 159px;" |
| + | |- | ||
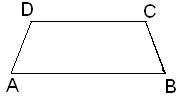
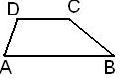
| + | | [[Image:Trapecio_isosceles.JPG|thumb|center|188x109px|Trapecio isósceles]]<br> | ||
| + | | [[Image:Trapecio_rectángulo.JPG|thumb|center|199x113px|Trapecio rectángulo]]<br> | ||
| + | | [[Image:Trapecio_escaleno.JPG|thumb|center|152x111px|Trapecio escaleno]]<br> | ||
| + | |} | ||
| − | + | El '''Isósceles '''tiene iguales los lados no paralelos. <br>El '''escaleno '''tiene los cuatro lados diferentes. Como se puede apreciar en la figura, el '''trapecio rectángulo''' es un caso especial de trapecio escaleno, pues, tiene uno de los lados no paralelos perpendicular a las bases. | |
| − | + | <br> | |
| − | + | '''''Trapezoides''''': No tienen ningún lado paralelo a su lado opuesto.<br> | |
| − | + | {| width="200" cellspacing="1" cellpadding="1" border="0" | |
| − | + | |- | |
| − | + | | [[Image:Trapezoide_simétrico.JPG|thumb|center|123x204px|Trapesoide simétrico]]<br> | |
| − | + | | [[Image:Trapezoide_asimétrico.JPG|thumb|center|259x196px|Trapezoide asimétrico]]<br> | |
| + | |} | ||
| − | <br> | + | El '''''Simétrico'''''tiene igual dos lados consecutivos, y también los otros dos. <br>El '''''Asimétrico'''''es aquel que no cumple con la condición anterior. |
| + | |||
| + | |||
| + | |||
| + | == Propiedades == | ||
| + | |||
| + | *La suma de los cuatro ángulos interiores equivale a cuatro rectos. | ||
| + | *Tiene dos diagonales en total, y desde un vértice se puede trazar solo una. | ||
| + | *Las diagonales de los convexos se cortan en un punto interior del cuadrilátero. | ||
== Ver también == | == Ver también == | ||
| − | <span style="display: none; | + | <span id="1284065516656S" style="display: none;"> </span> |
| − | <span style="display: none; | + | <span id="1284065514925S" style="display: none;"> </span> |
| − | <span style="display: none;" | + | <span id="1284065514910S" style="display: none;" />[[Triángulo|Triángulo]] |
[[Cuadrado|Cuadrado]] | [[Cuadrado|Cuadrado]] | ||
| − | [[Paralelogramo|Paralelogramo<br>]]<span style="display: none; | + | [[Paralelogramo|Paralelogramo]] |
| + | |||
| + | [[Rectángulo|Rectángulo<br>]]<span id="1284065514966E" style="display: none;"> </span> | ||
== Fuentes == | == Fuentes == | ||
| Línea 62: | Línea 83: | ||
[[Category:Geometría_euclídea]] | [[Category:Geometría_euclídea]] | ||
| + | |||
| + | <br> | ||
Revisión del 21:09 12 sep 2010
| ||||||
Cuadrilátero(Figura). Los cuadriláteros son los polígonos que tienen cuatro lados. Si te fijas, cerca de ti hay muchos objetos cuya línea de contorno tiene forma de cuadrilátero: una ventana, la pantalla de un ordenador o de un televisor plano, un póster, una puerta o el trapecio que forma en el suelo la luz del Sol que entra por la ventana. Los cuadriláteros son los polígonos que más abundan a nuestro alrededor, más que los triángulos y, por supuesto, que los pentágonos, hexágonos, etc.
Clasificación
Los cuadriláteros de forma general se clasifican en dos grandes grupos:
- vos: Son aquellos cuadriláteros, que al menos uno de sus lados cumple la condición de que la línea que lo contiene, divide a la figura en dos partes, o sea, la deja en ambos semiplanos en que divide la línea al plano.
- Convexos: Son aquellos cuadriláteros que cumplen la condición de que al prolongar cualquiera de sus lados, la línea que lo contiene deja al cuadrilátero en un solo semiplano.
Tipos
Los cuadriláteros se dividen en Paralelogramo, trapecios y Trapezoides.
Paralelogramos: Tienen sus dos pares de lados opuestos paralelos.
- El cuadradotiene los cuatro lados iguales y los cuatro ángulos rectos (90°).
- El rectángulotiene los lados iguales dos a dos y los cuatro ángulos rectos (90°).
- El rombotiene los cuatro lados iguales, pero sus ángulos no miden 90°.
- El romboidetiene los lados iguales dos a dos, pero sus ángulos no miden 90°.
Trapecios: Tienen un solo par de lados paralelos.
El Isósceles tiene iguales los lados no paralelos.
El escaleno tiene los cuatro lados diferentes. Como se puede apreciar en la figura, el trapecio rectángulo es un caso especial de trapecio escaleno, pues, tiene uno de los lados no paralelos perpendicular a las bases.
Trapezoides: No tienen ningún lado paralelo a su lado opuesto.
El Simétricotiene igual dos lados consecutivos, y también los otros dos.
El Asimétricoes aquel que no cumple con la condición anterior.
Propiedades
- La suma de los cuatro ángulos interiores equivale a cuatro rectos.
- Tiene dos diagonales en total, y desde un vértice se puede trazar solo una.
- Las diagonales de los convexos se cortan en un punto interior del cuadrilátero.
Ver también
Fuentes
- Microsoft ® Encarta ® 2007. © 1993--2006 Microsoft Corporation. Reservados todos los derechos.
- Miyares Arturo y Jose M Escalona. Geometría, Segundo Curso. Quinta Edición. Editorial Pueblo y Educación. La Habana. Cuba. 1974.