Magma (álgebra)
| ||||||
Magma (álgebra). Estructura algebraíca de la forma (A,*) donde A es un conjunto no vacío, en que se ha definido una operación binaria interna * , o bien una ley de composición o combinación interna [1]
Sumario
Introducción
En álgebra abstracta, un magma es un tipo especialmente elemental de estructura algebraica.
Específicamente, un magma consiste de un conjunto X con una sola operación binaria en el. Es, usualmente (pero no siempre), interpretado como una forma de multiplicación. Ningún axioma es impuesto a la operación al definir un magma. Los magmas no son usualmente estudiados como tales; sino que se consideran diferentes tipos de magmas, dependiendo de que axiomas se requieran de la operación.
Definiciones
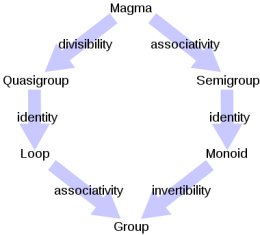
Tipos de magmas estudiados comúnmente incluyen:
- cuasigrupos -- magmas no vacíos donde la División es siempre posible;
- loop (álgebra)|loops -- cuasigrupos con elementos identidad;
- semigrupos -- magmas donde la operación es asociatividad;
- monoides -- semigrupos con elemento identidad;
- grupos -- monoides con elementos inversos, o equivalentemente, cuasigrupos asociativos (que son siempre loops);
- grupo abeliano -- grupos donde la operación es conmutatividad|conmutativa]].
El término "magma" fue introducido por Bourbaki. Previamente, el término "grupoide" fue común, y todavía es, a veces, utilizado. En esta enciclopedia, no obstante, reservamos "grupoide" para un concepto algebraico diferente, descrito en grupoide.
Hay lo que podemos llamar un magma libre sobre cualquier conjunto X. Puede ser descrito, en términos familiares en ciencias de la computación como el magma de los Árbol (programación) con operación dada por la yuxtaposición (ordenada) de los árboles por la raíz. Tiene por tanto un rol fundacional en sintaxis.
Más Definiciones
Un magma es llamado
- medial (álgebra) si satisface la identidad xy.uz=xu.yz (i.e. (x*y)*(u*z)=(x*u)*(y*z)),
- semimedial si satisface la identidad xx.yz=xy.xz,
- semimedial si satisface la identidad yz.xx=yx.zx,
- semimedial si es, a la vez, semimedial izquierdo y derecho,
- autodistributive si satisface la identidad x.yz=xy.xz,
- autodistributive si satisface la identidad yz.x=yx.zx,
- autodistributivo si es, a la vez, distributivo izquierdo y derecho,
- commutativo si satisface xy=yx,
- idempotente si satisface xx=x,
- unipotente si satisface xx=yy,
- zeropotente si satisface xx.y=yy.x=xx,
- alternativa (álgebra) si satisface xx.y=x.xy & x.yy=xy.y,
- un semigrupo si satisface x.yz=xy.z (asociatividad),
- un semigrupo con zeros izquierdos si satisface x=xy,
- un semigrupo con zeros derechos si satisface x=yx,
- un semigrupo con multiplicación nula si satisface xy=uv,
- entrópica (algebra) si es universal algebra de un magma cancelativo.
No Asociatividad
Una operación binaria * en un conjunto S que no satisfaga la ley asociativa se llama no-asociativa. Simbólicamente,para tal operación el orden de la evaluación importa. La substracción y la división de números reales son ejemplos bien conocidos de operaciones no-asociativas:
En general, se deben utilizar paréntesis para indicar el orden de la evaluación si aparece una operación no-asociativa más de una vez en una expresión. Sin embargo, los matemáticos convienen en una orden particular de la evaluación para varias operaciones no-asociativas comunes. Esto tiene el estatus de una convención, no de una verdad matemática. Una operación izquierdo-asociable se evalúa convencionalmente de izquierda a derecha, es decir, mientras que una operación derecho-asociable se evalúa convencionalmente de derecha a izquierda:
Las operaciones izquierdo-asociables y derecho-asociables ocurren; los ejemplos se dan abajo.
Más ejemplos
Las operaciones izquierdo-asociables incluyen las siguientes.
- Substracción y división de números reales:
Las operaciones derecho-asociables incluyen la siguiente.
- Exponenciación de números reales:
La razón por la que la exponenciación es derecho-asociable es que una operación izquierdo-asociable repetida del exponente sería menos útil. Múltiples apariciones se podrían reescribir con la multiplicación: (xy)z = x(yz).
- El operador de asignación en muchos lenguajes de programación es derecho-asociable.
Por ejemplo, en el lenguaje C
x = y = z; significa x = (y = z); y no (x = y) = z;
Es decir la declaración asignaría el valor de z a ambos x e y.
Las operaciones no-asociativas para las cuales no se define ningún orden convencional de la evaluación incluyen el siguiente.
- Tomar el promedio de números reales:
- Tomar el complemento relativo de conjuntos:
Véase También
Fuentes
Referencias
- ↑ Zamansky Marc Introducción al álgebra y análisis moderno Montaner y Simon, S.A. Barcelona (1967)