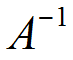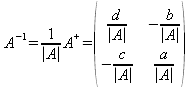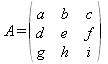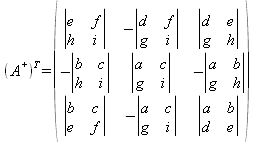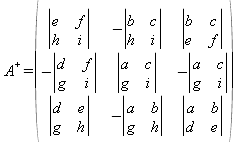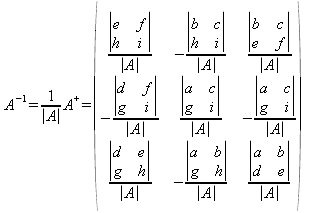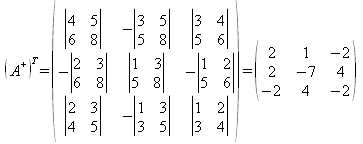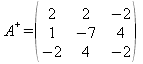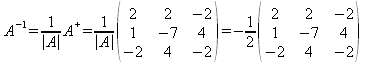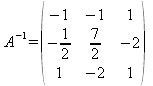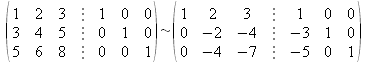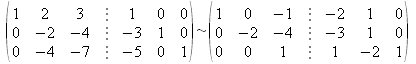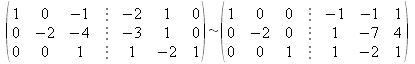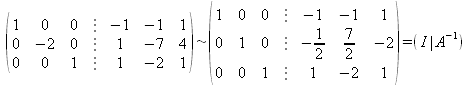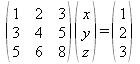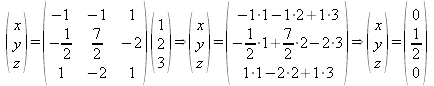Matriz inversa
| ||||||
Matriz inversa. Dícese de la Matriz cuadrada A-1 de orden N que dada, A una matriz cuadrada no singular del mismo orden, satisface AA-1=A-1A=IN.
Sumario
Definiciones.
Dada la matriz cuadrada A de orden N se dice que es una matriz inversible si y sólo si el determinante de A no es nulo.
Si A es una matriz inversible, se dice que la matriz cuadrada A-1 de orden N es la matriz inversa de A tal que AA-1=A-1A=IN.
Propiedades.
Relativas a la inversibilidad:
- Una matriz cuadrada A es inversible si existe otra matriz cuadrada B tal que AB=BA=I.
- Una matriz es inversible ssi:
- Es cuadrada.
- Es no singular.
- Si una matriz A de orden n es inversible, entonces su rango también es n.
- La matriz inversa si existe es única.
- (AB)-1=A-1B-1
- (AT)-1=(A-1)T
- (A-1)-1=A
- I-1=I
Métodos de obtención de matrices inversas
Mediante el determinante y la matriz adjunta:
- Sea A+ la matriz adjunta de A, A-1=A+/|A|.
Para los casos específicos de matrices inversibles de orden 2 y 3 puede calcularse sus inversas de la formas:
- Orden 2:
- Orden 3:
Método de Eliminación de Gauss-Jordan:
- A partir de se crea la matriz extendida (A|I) y mediante transformaciones elementales en cada fila, si A es inversible, se obtiene (I|A-1).
Solución de sistemas de ecuaciones líneales mediante la inversa
Sea la matriz A no singular y el sistema de ecuaciones lineales representado en la ecuación matricial:
- AX=B
Se puede multiplicar delante de ambos lados de la ecuación por A-1:
- A-1AX=A-1B => I.X=A-1B
de donde:
- X=A-1B
que muestra otra manera de determinar la solución de un sistema de ecuaciones lineales compatible.
Ejemplos.
La matriz:
| 1 | 2 | 3 |
| 4 | 5 | 6 |
| 7 | 8 | 9 |
no tiene inversa porque su determinante es 0, es decir es una matriz singular.
En cambio la matriz A:
| 1 | 2 | 3 |
| 3 | 4 | 5 |
| 5 | 6 | 8 |
cumple |A|=-2, es no singular y por ende es inversible. A-1 es:
| -1 | -1 | 1 |
| -0,5 | 3,5 | -2 |
| 1 | -2 | 1 |
La cual puede obtenerse mediante la matriz adjunta y su determinante:
O mediante el método de Jordan:
- Se escribe la matriz ampliada (A|I):
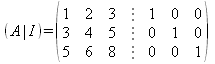 .
. - Pivote A1,1.
- Pivote A2,2.
- Pivote A3,3.
- Se divide la fila 2 por -2 y se obtiene finalmente (I|A-1):
Resolución de sistema de ecuaciones lineales
Sea el sistema de ecuaciones lineales representado por la ecuación matricial AX=B:
Pero la matriz que representa a los coeficientes del SEL tiene por inversa:
Y en este caso el sistema puede replantearse como X=A-1B, resolviéndose mediante el producto matricial:
Véase también
- Matriz
- Matriz cuadrada
- Matriz identidad
- Matriz adjunta
- Eliminación de Gauss-Jordan
- Matriz singular
- Determinante
Fuentes
- Colectivo de Autores. Álgebra lineal. Editorial Félix Varela, La Habana, 2003.
- K. Ribnikov. Análisis Combinatorio. Editorial Mir, Moscú, 1988.
- Matriz invertible en Wikipedia.