Optimización de funciones
| ||||
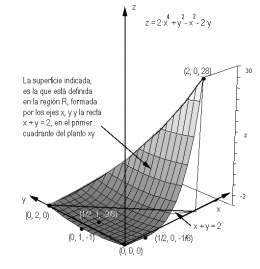
Optimización de funciones. Existe una amplia variedad de problemas y aplicaciones que tienen las siguientes finalidades: encuentra el área mínima, el menor coste, la forma óptima, la menor resistencia, el máximo beneficio, el mayor alcance...Todos estos problemas, se engloban dentro de la categoría de Optimización de funciones y pueden ser resueltos aplicando el cálculo diferencial.
Sumario
Problemas de optimización
Muchos de los problemas que se presentan en la práctica diariamente, están relacionados de una forma u otra, con encontrar los valores máximos y mínimos de una función, y más aún, determinar para qué valores de la variable independiente se alcanzan estos. Estos problemas se llaman, en general, problemas de optimización.
En términos generales, un problema de optimización consiste en encontrar el valor mínimo o minimizar, o encontrar el valor máximo o maximizar, una cierta función, de tal forma que satisfagan ciertas condiciones dadas.
La solución o soluciones óptimas son aquellas para las cuales se satisfacen las restricciones del problema y el valor de la función sea mínimo o máximo.
Pasos para la resolución de problemas de optimización
- Dibujar una figura de análisis (Si es necesario)
- Se plantea la función que hay que maximizar o minimizar.
- Se plantea una ecuación que relacione las distintas variables del problema, en el caso de que haya más de una variable.
- Se despeja una variable de la ecuación y se sustituye en la función de modo que nos quede una sola variable.
- Se deriva la función y se iguala a cero, para hallar los extremos locales.
- Se realiza la 2ª derivada para comprobar el resultado obtenido.
- Responder la pregunta del problema.
Ejemplo1:
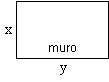
Se necesita una superficie rectangular cercada por tres lados con tela metálica y por el cuarto lado con un muro de piedra. Se dispone de 20 metros lineales de tela metálica. Calcula las dimensiones queha de tener la superficie para que su área sea la mayor posible.
Resolución
En la figura aparece representada la superficie.
Su área es A =x.y siendo x, y los lados del rectángulo.
Como se dispone de 20 metros de tela metálica, entonces x+y+x=20 es decir y=20-2x
A= x.y = x(20-2x) = 20x-2x2 con 0<=x<=10
Hallamos el máximo de la función A.
A´(x)=20-4x
20-4x=0
x=5
A´´(x)=-4 para todo x, por lo que en x=5 hay un máximo. Este máximo lo comparamos con los valores de los extremos del interalo:
A(0)=0 , A(10)= 0
Luego el máximo es absoluto y es el valor buscado
El valor de y=20-2(5)=10
Rta. El lado cercado por el muro debe medir 10 m y el otro lado 5m.
Ejemplo 2:
Ejemplo 3:
El costo total de producción de x unidades de un producto es CT =5/2 x2+20x en pesos y el precio unitario es p=50-x/2 pesos. Halle el número de unidades que se deben vender para que la ganancia sea máxima.
CT =5/2 x2+20x
p=50-x/2 I(x)=x.(50-x/2 )=50x-x2/2
G(x)=I(x)-CT
G(x)= 50x-x2/2 -(5/2 x2+20x)
G(x)=30x-3x2
G´(x)=30-6x
30-6x=0
x=5 Rta. El número de unidades que se deben vender es de 5.
Fuente
- Libro de texto Matemática onceno grado
- Problemas de optimización