¿No sabes por dónde empezar? Ayúdanos normalizando artículos.
¿Tienes experiencia? Crea alguno de estos artículos de actualidad.
Diferencia entre revisiones de «Desigualdad triangular»
(→Importancia.) |
|||
| Línea 18: | Línea 18: | ||
La variante de en lugar de la desigualdad estricta usar una semidesigualdad (menor o igual) se emplea en algunas métricas y definiciones de estructuras matemáticas. | La variante de en lugar de la desigualdad estricta usar una semidesigualdad (menor o igual) se emplea en algunas métricas y definiciones de estructuras matemáticas. | ||
| − | ==Importancia | + | ==Importancia== |
La desigualdad triangular permite definir que tres segmentos ''a'', ''b'', ''c'' puedan conformar o no un triángulo. A continuación aparece un fragmento de código [[Python]] donde aparece una [[función]] [[Booleano|booleana]] que determina si dichos segmentos pueden conformar los lados de un triángulo aplicando la desigualdad triangular. | La desigualdad triangular permite definir que tres segmentos ''a'', ''b'', ''c'' puedan conformar o no un triángulo. A continuación aparece un fragmento de código [[Python]] donde aparece una [[función]] [[Booleano|booleana]] que determina si dichos segmentos pueden conformar los lados de un triángulo aplicando la desigualdad triangular. | ||
| Línea 26: | Línea 26: | ||
</pre> | </pre> | ||
| − | ===Métricas | + | ===Métricas=== |
Es una de las propiedades básicas que sirve desde los puntos de vista algebraico, geométrico para identificar a las métricas o distancias. | Es una de las propiedades básicas que sirve desde los puntos de vista algebraico, geométrico para identificar a las métricas o distancias. | ||
| Línea 33: | Línea 33: | ||
* ''d(a,b)<d(a,c)+d(c,b)'' para cualesquiera 3 objetos ''a'', ''b'', ''c''. | * ''d(a,b)<d(a,c)+d(c,b)'' para cualesquiera 3 objetos ''a'', ''b'', ''c''. | ||
| − | ====Métrica discreta | + | ====Métrica discreta==== |
Sea la [[Métrica discreta]] definida como sigue: | Sea la [[Métrica discreta]] definida como sigue: | ||
| Línea 45: | Línea 45: | ||
''<=> 1<2'' (Verdadero). | ''<=> 1<2'' (Verdadero). | ||
| − | ====Métrica euclideana | + | ====Métrica euclideana==== |
Sea la [[Métrica euclideana]] o distancia euclideana definida según la expresión: | Sea la [[Métrica euclideana]] o distancia euclideana definida según la expresión: | ||
Revisión del 14:46 2 abr 2012
| ||||||
Desigualdad triangular. Axioma que define la característica de que entre dos puntos distintos la menor distancia es el segmento de recta que los une.
En el caso de los triángulos, indica que cualquier lado siempre es menor en longitud que la suma de los restantes.
Esta propiedad sirve también para caracterizar las métricas o distancias que a la larga definen las estructuras de tipo topológica y diversas geometrías
Sumario
[ocultar]Definición
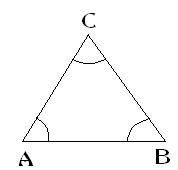
Sean tres puntos A, B, C no alineados se cumple siempre:
- |AB|<|BC|+|AC|.
- |AC|<|AB|+|BC|.
- |BC|<|AB|+|AC|.
A esta propiedad se denomina Desigualdad triangular.
La variante de en lugar de la desigualdad estricta usar una semidesigualdad (menor o igual) se emplea en algunas métricas y definiciones de estructuras matemáticas.
Importancia
La desigualdad triangular permite definir que tres segmentos a, b, c puedan conformar o no un triángulo. A continuación aparece un fragmento de código Python donde aparece una función booleana que determina si dichos segmentos pueden conformar los lados de un triángulo aplicando la desigualdad triangular.
def Lados_Triangulo(a,b,c):
return (a<b+c) and (b<a+c) and (c<a+b)
Métricas
Es una de las propiedades básicas que sirve desde los puntos de vista algebraico, geométrico para identificar a las métricas o distancias.
En cualquier caso si d es una métrica debe satisfacer la desiguladad triangular:
- d(a,b)<d(a,c)+d(c,b) para cualesquiera 3 objetos a, b, c.
Métrica discreta
Sea la Métrica discreta definida como sigue:
- d(x,y)=0 si x=y.
- d(x,y)=1 si no.
para a, b, c objetos distintos se cumple siempre la desigualdad triangular:
d(a,b)<d(a,c)+d(c,b)
<=> 1<1+1
<=> 1<2 (Verdadero).
Métrica euclideana
Sea la Métrica euclideana o distancia euclideana definida según la expresión:
donde A=(a1;a2;...;an) y B=(b1;b2;...;bn).
Si además se tiene otro punto C=(c1;c2;...;cn). También se cumple:
d(A,B)<d(A,C)+d(C,B)
Fuentes.
- I. Bronshtein, K. Semendiaev. Manual de matemáticas para ingenieros y estudiantes. 2da Edición. Editorial Mir, Moscú. 1973.
- K. Ribnikov. Análisis Combinatorio. Editorial Mir. Moscú, 1988. Páginas 17-23.
- Desigualdad_triangular en Wikipedia. Revisado 25 de marzo de 2012.
- Distancia en Wikipedia. Revisado 25 de marzo de 2012.
