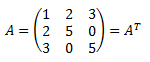Diferencia entre revisiones de «Matriz simétrica»
(Nuevo artículo) |
|||
| Línea 2: | Línea 2: | ||
<div align="justify"> | <div align="justify"> | ||
| − | '''Matriz simétrica'''. Dícese de la [[matriz]] cuadrada que es igual a su [[traspuesta| | + | '''Matriz simétrica'''. Dícese de la [[matriz]] cuadrada que es igual a su [[Matriz traspuesta|traspuesta]]. |
==Definición== | ==Definición== | ||
Revisión del 02:16 16 abr 2018
| ||||||
Matriz simétrica. Dícese de la matriz cuadrada que es igual a su traspuesta.
Definición
Seaa A una matriz cuadrada de dimensión m. Si se denota por A(i,j) el elemento de la fila i y columna j de A, entonces la matriz A es simétrica si A(i,j)=A(j,i).
Ejemplo: la matriz identidad es una matriz simétrica.
Propiedades
- La inversa de una matriz simétrica regular es simétrica.
- La matriz adjunta de una matriz simétrica es simétrica.
- La suma de simétricas es simétrica. El producto lo es si, y sólo si, también es conmutativo.
- Los autovalores (valores propios) de una matriz cuadrada, real y simétrica son reales.
- Una matriz cuadrada y real, A, es simétrica si, y sólo si, es diagonalizable mediante una matriz de paso ortogonal, Q.