Diferencia entre revisiones de «Anillo (álgebra)»
m (Julio Fermit movió la página Anillo algebraico a Anillo (Álgebra): En esta disciplina, existe un sistema algebraico formado por un conjunto y dos operaciones, inicialmente sin adjetivo alguno) |
(→Referencias: categoría que abarca campos, grupos, anillos, espacios vectoriales, k-módulos, álgebra (estructura)) |
||
| (No se muestran 11 ediciones intermedias de 4 usuarios) | |||
| Línea 1: | Línea 1: | ||
{{Definición|nombre=Anillo algebraico|imagen=Matemática.jpg|concepto=Estructura algebraica de un conjunto no vacío y dos operaciones ''*'', ''@'' sobre éste cerradas y asociativas, ''*'' es conmutativa y en ella se verifica la existencia del neutro y los inversos para cada elemento del conjunto y juntas ''*'' y ''@'' satisfacen la distributividad.}} | {{Definición|nombre=Anillo algebraico|imagen=Matemática.jpg|concepto=Estructura algebraica de un conjunto no vacío y dos operaciones ''*'', ''@'' sobre éste cerradas y asociativas, ''*'' es conmutativa y en ella se verifica la existencia del neutro y los inversos para cada elemento del conjunto y juntas ''*'' y ''@'' satisfacen la distributividad.}} | ||
| − | + | '''Anillo'''. En caso de posibilidad de confusión (anillo topológico) o si se trata de destacar las dos operaciones ínsitas a su estructura, es llamado también '''anillo algebraico''' <ref>Pontriaguin: ''Grupos continuos'' Editorial URSS, Moscú 1994 </ref>. | |
| − | '''Anillo | + | En [[álgebra]], un '''anillo ''' es cualquier conjunto R no vacío con dos operaciones de composición interna, siendo con la primera un grupo abeliano y la segunda operación asociativa y además distributiva respecto de la primera. |
| − | + | Si se da la situación de que la segunda operación sea conmutativa se le nombra ''anillo conmutativo'' y si hubiera un elemento identidad para la segunda operación se llama anillo unitario <ref>Kostrikin: Introducción al álgebra </ref>. Para el caso, el anillo de los cuaternios es un anillo unitario y no conmutativo y el anillo de los enteros pares es un anillo conmutativo sin unidad. | |
| − | Si '' | + | Si no hay posibilidad de confusión a la primera operación del anillo se llama ''adición'' y a la segunda, ''multiplicación'', que son la generalización de las dos operaciones que aparecen en los sistemas numéricos y se denota la suma como a+b y el producto, como ab, siendo a y b cualesquier elementos del anillo R. |
==Definición== | ==Definición== | ||
| Línea 26: | Línea 26: | ||
* Sea A un conjunto no vacío con dos operaciones binarias ''*'' y ''@'' es un '''anillo''' si y sólo si ''<A,*>'' es un [[grupo abeliano]], ''<A,@>'' es un [[monoide]] y se satisface la ley distributiva ''x@(y*z)=(x@y)*(x@z)'' para todos ''x'', ''y'', ''z'' de ''A'' | * Sea A un conjunto no vacío con dos operaciones binarias ''*'' y ''@'' es un '''anillo''' si y sólo si ''<A,*>'' es un [[grupo abeliano]], ''<A,@>'' es un [[monoide]] y se satisface la ley distributiva ''x@(y*z)=(x@y)*(x@z)'' para todos ''x'', ''y'', ''z'' de ''A'' | ||
| + | |||
| + | ==Definición alternativa 1== | ||
| + | Un conjunto S se denomina '''anillo''', si se han definido sobre él dos operaciones , denominadas ''adición'' y ''multiplicación'', siendo ambas conmutativas y asociativas, y vinculadas por la ley distributiva, conllevando además la adición la ''operación inversa'', denominada ''resta''. <ref>A.G. Kurosch. ''Curso de álgebra superior''. Editorial Mir, Moscú (1981) Impreso en la URSS. Traducido del ruso por Emiliano APARICIO BERNARDO </ref> | ||
| + | |||
| + | ==Definición alternativa 2== | ||
| + | Sea el conjunto R un conjunto no vacío de diversa naturaleza, sea numérica, geométrica, matricial, aplicaciones, con dos operaciones algebraicas independientes, que se llamarán ''adición'', denotada por + y ''multiplicación'', indicada por yuxtaposición, si se cumple lo siguiente: | ||
| + | # El conjunto R con la adición es un grupo abeliano. | ||
| + | # El conjunto R con la multiplicación es un semigrupo | ||
| + | # L a multiplicacción es distributiva respecto de la adicióna(b + c) = ab + ac, (a + b)c = ac + bc, | ||
| + | El conjunto R que cumple las tres condiciones anteriormente señaladas se denomina '''anillo'''. R provisto de dos operaciones es un sistema algebraico más complejo que el grupo. <ref>A. I. Kostrikin '' Introducción al álgebra'' Editorial Mir Moscú (1983) </ref> | ||
==Ejemplos== | ==Ejemplos== | ||
| Línea 40: | Línea 50: | ||
# Todo [[cuerpo algebraico|cuerpo]] ''<C,*,@>'' es también un anillo. | # Todo [[cuerpo algebraico|cuerpo]] ''<C,*,@>'' es también un anillo. | ||
# Por tanto los [[Conjunto numérico|conjuntos numéricos]] [[Número racional|racionales]], [[Número real|reales]] y [[Número complejo|complejos]] que son cuerpos con la suma y la [[multiplicación]] también se constituyen en anillos sobre esas mismas operaciones. | # Por tanto los [[Conjunto numérico|conjuntos numéricos]] [[Número racional|racionales]], [[Número real|reales]] y [[Número complejo|complejos]] que son cuerpos con la suma y la [[multiplicación]] también se constituyen en anillos sobre esas mismas operaciones. | ||
| + | |||
| + | ==Otros ejemplos== | ||
| + | * El conjunto P de los números enteros pares, provisto de las usuales operaciones de adición y multiplicación de números enteros es un anillo. | ||
| + | * El conjunto de polinomios en la ''indeterminada'' ''x'' con coeficientes de un campo numérico prouesto, inclusive de un anillo numérico dado. | ||
| + | * Tomemos el conjunto de las funciones , determinadas para '''todos''' los valores reales de ''t'' y que toman valores reales. En él se definen '' la suma'' de las funciones f(t) y h(t) será la función cuyo valor para cualquier t = t<sub>0</sub> será igual a la suma de los valores de las funciones dadas, esto es, f(t<sub>0</sub>) +g(t<sub>0</sub>); el ''producto'' de estas funciones será una función cuyo valor para cualquie t = t<sub>0</sub> será igual a f(t<sub>0</sub>) . g(t<sub>0</sub>). En este caso se puede comprobar que se cumplen los requisitos para ser anillo; la ''diferencia'' de funciones en t = t<sub>0</sub> es la función cuyo valor es f(t<sub>0</sub>) - g(t<sub>0</sub>). | ||
| + | |||
| + | ==Divisores de cero== | ||
| + | En el anillo de matrices cuadradas de orden 2 hay matrices K y L, ninguna igual a la matriz 0, pero el KL =0; s i se da este caso en algunos anillos, se dice que los elementos a ≠ 0 y b ≠ 0, pero ab = 0, dice que a es divisor por izquierda de 0 y b, divisor por derecha de 0; en caso de ser el anillo conmutativo, tanto a ''a''como a ''b'' se les nombra '''divisores de 0''' <ref> Birkhoff y Mc Lane: ''Álgebra Moderna''</ref>. | ||
==Fuentes== | ==Fuentes== | ||
*Carl B. Allendoerfer, Cletus O. Oakley. Introducción moderna a la [[Matemáticas superiores|matemática superior]]. Ediciones del Castillo, [[Madrid]]. [[1967]]. | *Carl B. Allendoerfer, Cletus O. Oakley. Introducción moderna a la [[Matemáticas superiores|matemática superior]]. Ediciones del Castillo, [[Madrid]]. [[1967]]. | ||
| + | * Fraleigh: ''Álgebra abstracta'' | ||
| + | * Robinson Castro Puche: ''Álgebra Moderna e introducción al álgebra geométrica''. | ||
| + | *Nieto: ''Álgebra elemental'', ediciones de OEA, Washington D. C. | ||
| + | |||
| + | ==Referencias== | ||
| + | <references /> | ||
| − | [[Categoría: | + | [[Categoría:Sistemas algebraicos]][[Categoría:Álgebra]][[Categoría:Matemáticas]] |
última versión al 10:12 9 oct 2019
Anillo. En caso de posibilidad de confusión (anillo topológico) o si se trata de destacar las dos operaciones ínsitas a su estructura, es llamado también anillo algebraico [1]. En álgebra, un anillo es cualquier conjunto R no vacío con dos operaciones de composición interna, siendo con la primera un grupo abeliano y la segunda operación asociativa y además distributiva respecto de la primera.
Si se da la situación de que la segunda operación sea conmutativa se le nombra anillo conmutativo y si hubiera un elemento identidad para la segunda operación se llama anillo unitario [2]. Para el caso, el anillo de los cuaternios es un anillo unitario y no conmutativo y el anillo de los enteros pares es un anillo conmutativo sin unidad.
Si no hay posibilidad de confusión a la primera operación del anillo se llama adición y a la segunda, multiplicación, que son la generalización de las dos operaciones que aparecen en los sistemas numéricos y se denota la suma como a+b y el producto, como ab, siendo a y b cualesquier elementos del anillo R.
Sumario
Definición
Sea un conjunto A no vacío y las operaciones binarias * y @ que satisfacen los siguientes axiomas:
- Clausura de *:
 . * es cerrada.
. * es cerrada. - Asociatividad de *: Para todos x, y, z de A, (x*y)*z=x*(y*z).
- Conmutitividad de *: Para todos x e y en A se cumple x*y=y*x.
- Existencia del neutro: Existe uno y solo un elemento e de A tal que para todo x de A se cumple que x*e=e*x=x. e es llamado neutro para * en A.
- Existencia de los inversos: Para todo x en A, existe un único elemento x" también en A, que satisface x*x"=x"*x=e. A x" se denomina inverso de x según *.
- Clausura de @:
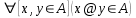 . * es cerrada.
. * es cerrada. - Asociatividad de @*: Para todos x, y, z de A, (x@y)@z=x@(y@z).
- Distributividad: Para todos x, y, z de A, x@(y*z)=x@y * x@z.
Se dice que A con las operaciones * y @ es un anillo.
El incumplimiento de cualquiera de los axiomas precedentes inhabilita la condición de anillo.
Apoyándose en otras definiciones del álgebra puede decirse que:
- Sea A un conjunto no vacío con dos operaciones binarias * y @ es un anillo si y sólo si <A,*> es un grupo abeliano, <A,@> es un monoide y se satisface la ley distributiva x@(y*z)=(x@y)*(x@z) para todos x, y, z de A
Definición alternativa 1
Un conjunto S se denomina anillo, si se han definido sobre él dos operaciones , denominadas adición y multiplicación, siendo ambas conmutativas y asociativas, y vinculadas por la ley distributiva, conllevando además la adición la operación inversa, denominada resta. [3]
Definición alternativa 2
Sea el conjunto R un conjunto no vacío de diversa naturaleza, sea numérica, geométrica, matricial, aplicaciones, con dos operaciones algebraicas independientes, que se llamarán adición, denotada por + y multiplicación, indicada por yuxtaposición, si se cumple lo siguiente:
- El conjunto R con la adición es un grupo abeliano.
- El conjunto R con la multiplicación es un semigrupo
- L a multiplicacción es distributiva respecto de la adicióna(b + c) = ab + ac, (a + b)c = ac + bc,
El conjunto R que cumple las tres condiciones anteriormente señaladas se denomina anillo. R provisto de dos operaciones es un sistema algebraico más complejo que el grupo. [4]
Ejemplos
- Los números enteros son un anillo de la forma
 .
. - Sea Mn el conjunto de las matrices cuadradas de orden n, puede decirse que
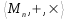 es un anillo.
es un anillo.
- Para todas las matrices cuadradas de n filas A y B A+B también es una matriz cuadrada de n filas y columnas.
- La suma de matrices cuadradas del mismo orden n es asociativa.
- La suma de matrices cuadradas del mismo orden n es conmutativa.
 es el neutro para la suma.
es el neutro para la suma.- Para toda matriz cuadrada de n filas y columnas
 se tiene su inverso dado por
se tiene su inverso dado por  y según la suma de matrices
y según la suma de matrices  .
. - El producto de matrices cuadradas de orden n es cerrado.
- El producto de matrices cuadradas de orden n es asociativo.
- Para todas matrices cuadradas de orden n A, B, C se cumple A(B+C)=AB+AC.
- Todo cuerpo <C,*,@> es también un anillo.
- Por tanto los conjuntos numéricos racionales, reales y complejos que son cuerpos con la suma y la multiplicación también se constituyen en anillos sobre esas mismas operaciones.
Otros ejemplos
- El conjunto P de los números enteros pares, provisto de las usuales operaciones de adición y multiplicación de números enteros es un anillo.
- El conjunto de polinomios en la indeterminada x con coeficientes de un campo numérico prouesto, inclusive de un anillo numérico dado.
- Tomemos el conjunto de las funciones , determinadas para todos los valores reales de t y que toman valores reales. En él se definen la suma de las funciones f(t) y h(t) será la función cuyo valor para cualquier t = t0 será igual a la suma de los valores de las funciones dadas, esto es, f(t0) +g(t0); el producto de estas funciones será una función cuyo valor para cualquie t = t0 será igual a f(t0) . g(t0). En este caso se puede comprobar que se cumplen los requisitos para ser anillo; la diferencia de funciones en t = t0 es la función cuyo valor es f(t0) - g(t0).
Divisores de cero
En el anillo de matrices cuadradas de orden 2 hay matrices K y L, ninguna igual a la matriz 0, pero el KL =0; s i se da este caso en algunos anillos, se dice que los elementos a ≠ 0 y b ≠ 0, pero ab = 0, dice que a es divisor por izquierda de 0 y b, divisor por derecha de 0; en caso de ser el anillo conmutativo, tanto a acomo a b se les nombra divisores de 0 [5].
Fuentes
- Carl B. Allendoerfer, Cletus O. Oakley. Introducción moderna a la matemática superior. Ediciones del Castillo, Madrid. 1967.
- Fraleigh: Álgebra abstracta
- Robinson Castro Puche: Álgebra Moderna e introducción al álgebra geométrica.
- Nieto: Álgebra elemental, ediciones de OEA, Washington D. C.
Referencias
- ↑ Pontriaguin: Grupos continuos Editorial URSS, Moscú 1994
- ↑ Kostrikin: Introducción al álgebra
- ↑ A.G. Kurosch. Curso de álgebra superior. Editorial Mir, Moscú (1981) Impreso en la URSS. Traducido del ruso por Emiliano APARICIO BERNARDO
- ↑ A. I. Kostrikin Introducción al álgebra Editorial Mir Moscú (1983)
- ↑ Birkhoff y Mc Lane: Álgebra Moderna
