Diferencia entre revisiones de «Ley de los senos»
(Página creada con 'La Ley de los senos desempeña un papel fundamental en la solución de Triángulos oblicuos(Triángulos sin ángulo recto). Esta ley proporciona la herramienta bási...') |
m (Texto reemplazado: «<div align="justify">» por «») |
||
| (No se muestran 4 ediciones intermedias de 3 usuarios) | |||
| Línea 1: | Línea 1: | ||
| − | |||
| − | |||
{{Definición | {{Definición | ||
|nombre=Ley de los senos | |nombre=Ley de los senos | ||
| − | |imagen= | + | |imagen=Lawofsines.gif |
|tamaño= | |tamaño= | ||
| − | |concepto=La razón del Seno de un ángulo con su lado opuesto | + | |concepto= La razón del Seno de un ángulo con su lado opuesto es igual a la razón del Seno de cualquiera de los otros ángulos con su lado opuesto. |
| − | + | }} | |
| − | + | '''Ley de los senos'''. Desempeña un papel fundamental en la solución de [[Triángulos oblicuos]] ([[Triángulos]] sin ángulo recto). Esta ley proporciona la herramienta básica para la solución de Triángulos oblicuos. Si las cantidades dadas incluyen un lado y el [[ángulo opuesto]], se debe usar la [[Ley]] de los senos de otro modo se inicia con la [[Teorema del coseno|Ley de los cosenos]]. | |
| − | }} | ||
| − | == | + | == Deducción de la ley == |
| − | La ley de los | + | La ley de los senos es relativamente fácil de probar usando las propiedades de los [[Triángulo rectángulo|Triángulos rectángulos]]. Se usará también el hecho de que sen(180-X)=sen X , lo cual se obtiene fácilmente usando una [[Identidad]] de la diferencia. |
| − | Refiriéndose a los siguientes triángulos se procede como sigue: | + | Refiriéndose a los siguientes triángulos se procede como sigue: |
| − | [[Image: | + | [[Image:Ley_de_los_senos.svg.png|right|419x367px|Demostración ley senos1.JPG]]sen α=h/a y sen δ=h/b<br> |
Despejando h de cada [[Ecuación]] se obtiene:<br> | Despejando h de cada [[Ecuación]] se obtiene:<br> | ||
| Línea 28: | Línea 25: | ||
sen α / b=sen δ / a (1)<br> | sen α / b=sen δ / a (1)<br> | ||
| − | De manera similar, para cada | + | De manera similar, para cada triángulo:<br> |
sen α=m/c y sen α=sen(180-α) <br> | sen α=m/c y sen α=sen(180-α) <br> | ||
| Línea 34: | Línea 31: | ||
sen α=m/c y sen α=m/b<br> | sen α=m/c y sen α=m/b<br> | ||
| − | Al despejar m de cada | + | Al despejar m de cada Ecuación, se obtiene:<br> |
m=c * sen α y m=b * sen α<br> | m=c * sen α y m=b * sen α<br> | ||
| Línea 44: | Línea 41: | ||
sen α / b=sen α / c (2)<br> | sen α / b=sen α / c (2)<br> | ||
| − | Si se combinan las | + | Si se combinan las ecuaciones (1) y (2), se obtiene la ley de los senos. |
| − | == | + | == Teorema == |
| − | Ley de los senos: | + | Ley de los senos: |
| − | [[Image:Teorema ley senos.JPG|245x164px|Teorema ley | + | [[Image:Teorema ley senos.JPG|245x164px|Teorema ley senos.JPG]] |
| − | En otras palabras, la razón del | + | En otras palabras, la razón del seno de un ángulo con su lado opuesto es igual a la razón del seno de cualquiera de los otros ángulos con su lado opuesto. |
| − | Por consiguiente, la ley de los | + | Por consiguiente, la ley de los senos se usa para resolver Triángulos, dando: |
| − | #Dos lados y un ángulo opuesto a uno de ellos(LLA). | + | #Dos lados y un ángulo opuesto a uno de ellos(LLA). |
| − | #Dos ángulos y cualquier lado(ALA o AAL). | + | #Dos ángulos y cualquier lado(ALA o AAL). |
| − | == | + | == Solución para el caso ALA == |
| − | [[Image:Teorema ley senos.JPG|right|233x155px|Teorema ley senos.JPG]]Para los valores α=45<sup>0</sup> , γ=28<sup>0</sup> y b=120 m | + | [[Image:Teorema ley senos.JPG|right|233x155px|Teorema ley senos.JPG]]Para los valores α=45<sup>0</sup> , γ=28<sup>0</sup> y b=120 m |
| − | Solución: | + | Solución: |
| − | Se están dando dos ángulos y el lado que los contiene, este es el caso ALA. Encuentre el tercer ángulo, después encuentre los otros dos lados usando la ley de los senos. | + | Se están dando dos ángulos y el lado que los contiene, este es el caso ALA. Encuentre el tercer ángulo, después encuentre los otros dos lados usando la ley de los senos. |
| − | Despeje β: | + | Despeje β: |
α + β + γ =180<sup>0</sup> <br> | α + β + γ =180<sup>0</sup> <br> | ||
| Línea 131: | Línea 128: | ||
== Fuentes == | == Fuentes == | ||
| − | *Raymond A. Barnett, Michael R. Ziegler, Karl E. Byleen. [[Precálculo]]: | + | *Raymond A. Barnett, Michael R. Ziegler, Karl E. Byleen. [[Precálculo]]: Funciones y Gráficas Volumen 2 |
[[Category:Fundamentos_de_la_Geometría]] | [[Category:Fundamentos_de_la_Geometría]] | ||
última versión al 03:07 27 ago 2019
| ||||||
Ley de los senos. Desempeña un papel fundamental en la solución de Triángulos oblicuos (Triángulos sin ángulo recto). Esta ley proporciona la herramienta básica para la solución de Triángulos oblicuos. Si las cantidades dadas incluyen un lado y el ángulo opuesto, se debe usar la Ley de los senos de otro modo se inicia con la Ley de los cosenos.
Sumario
Deducción de la ley
La ley de los senos es relativamente fácil de probar usando las propiedades de los Triángulos rectángulos. Se usará también el hecho de que sen(180-X)=sen X , lo cual se obtiene fácilmente usando una Identidad de la diferencia.
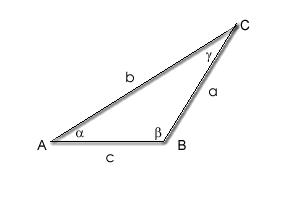
Refiriéndose a los siguientes triángulos se procede como sigue:
sen α=h/a y sen δ=h/b
Despejando h de cada Ecuación se obtiene:
h=a * sen α y h=b * sen δ
Así,
a * sen α=b * sen δ
sen α / b=sen δ / a (1)
De manera similar, para cada triángulo:
sen α=m/c y sen α=sen(180-α)
sen α=m/c y sen α=m/b
Al despejar m de cada Ecuación, se obtiene:
m=c * sen α y m=b * sen α
Así,
c * sen α=b * sen α
sen α / b=sen α / c (2)
Si se combinan las ecuaciones (1) y (2), se obtiene la ley de los senos.
Teorema
Ley de los senos:
En otras palabras, la razón del seno de un ángulo con su lado opuesto es igual a la razón del seno de cualquiera de los otros ángulos con su lado opuesto.
Por consiguiente, la ley de los senos se usa para resolver Triángulos, dando:
- Dos lados y un ángulo opuesto a uno de ellos(LLA).
- Dos ángulos y cualquier lado(ALA o AAL).
Solución para el caso ALA
Para los valores α=450 , γ=280 y b=120 m
Solución:
Se están dando dos ángulos y el lado que los contiene, este es el caso ALA. Encuentre el tercer ángulo, después encuentre los otros dos lados usando la ley de los senos.
Despeje β:
α + β + γ =1800
β=1800 - (α + γ)
=1800 -(280 + 450)
=1060
Despeje c:
sen β / b=sen γ / c
c=(b * sen γ) / sen β
=(1200 * sen 280) / sen 1060
=58,6 m
Despeje a:
sen α / a=sen β / b
a=(b * sen α) / sen β
=(1200 * sen 450) / sen 1060
=88,3 m
Solución para el caso LLA
Para los valores β=1230 , b=47 cm y c=23 cm:
Despeje γ:
sen β / b=sen γ / c
sen γ=(c * sen β) / b
γ=sen-1[(230 * sen 1230) / 470]
=240
Despeje α:
α + β + γ = 1800
α=1800 - 1230 -240
=330
Despeje a:
sen β / b=sen α / a
a=(b * sen α) / sen 1230
=(470 * sen 330) / sen 1230
=31 cm
Fuentes
- Raymond A. Barnett, Michael R. Ziegler, Karl E. Byleen. Precálculo: Funciones y Gráficas Volumen 2