Diferencia entre revisiones de «Cisoide de Diocles»
(Página creada con '{{Desarrollo}} {{Definición |nombre=Cisoide de Diocles |imagen=Cisoide.gif |tamaño= |concepto= }} <div align="justify"> '''Cisoide de Diocles'''. Es el [http://es.wikipedia.o...') |
m (Texto reemplazado: «<div align="justify">» por «») |
||
| (No se muestran 8 ediciones intermedias de 3 usuarios) | |||
| Línea 1: | Línea 1: | ||
| − | |||
{{Definición | {{Definición | ||
|nombre=Cisoide de Diocles | |nombre=Cisoide de Diocles | ||
| − | |imagen= | + | |imagen=Cisoide_de_Diocles.jpg |
|tamaño= | |tamaño= | ||
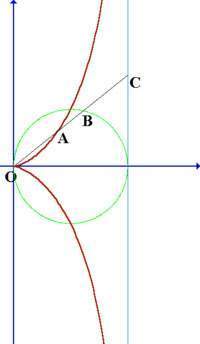
| − | |concepto= | + | |concepto= Cisoide de Diocles (línea roja). El segmento OA es igual a OC menos OB. |
}} | }} | ||
| − | + | ||
| − | '''Cisoide de Diocles'''. | + | '''Cisoide de Diocles'''. [[cisoide]] generado por el vector posición de una recta paralela al eje OY (Curva 1), que pasa por el punto (2a,0), al que se le resta el radio vector de una [[Circunferencia|circunferencia]] de radio a y centro en (0,a)(Curva 2). |
== Historia == | == Historia == | ||
| − | |||
[[Diocles]] fue un matemático [[Griego|griego]] que ideó esta curva con el objetivo de resolver el problema de la duplicación del [[Cubo|cubo]]. | [[Diocles]] fue un matemático [[Griego|griego]] que ideó esta curva con el objetivo de resolver el problema de la duplicación del [[Cubo|cubo]]. | ||
| Línea 16: | Línea 14: | ||
== Definición == | == Definición == | ||
| − | La cisoide se define como el lugar geométrico de los puntos C que verifican que | | + | La cisoide se define como el [http://es.wikipedia.org/wiki/Lugar_geom%C3%A9trico lugar geométrico] de los puntos C que verifican que |OA| = |BC|. |
== Ecuaciones == | == Ecuaciones == | ||
| − | + | * Su [[Ecuación|ecuación]] cartesiana es: | |
| − | * [[Ecuación|ecuación]] cartesiana: | ||
[[Image:EcuaccartianCisoide.png]] | [[Image:EcuaccartianCisoide.png]] | ||
| Línea 32: | Línea 29: | ||
[[Image:Ecuaccoordenadaspolares_cisoide.png]] | [[Image:Ecuaccoordenadaspolares_cisoide.png]] | ||
| − | |||
== Vea también == | == Vea también == | ||
| − | |||
*[[Parábola|Parábola]] | *[[Parábola|Parábola]] | ||
| − | |||
*[[Hipérbola|Hipérbola]] | *[[Hipérbola|Hipérbola]] | ||
| − | |||
*[[Circunferencia|Circunferencia]] | *[[Circunferencia|Circunferencia]] | ||
| − | |||
*[[Elipse|Elipse]] | *[[Elipse|Elipse]] | ||
| − | |||
*[[Estrofoide|Estrofoide]] | *[[Estrofoide|Estrofoide]] | ||
== Fuentes == | == Fuentes == | ||
| − | + | * Cisoide de Diocles. Disponible en:[http://personales.ya.com/jmreyes/curvas1.html Personales ya]. Citado [[8 de agosto]] de [[2011]] | |
| − | * Cisoide de Diocles | + | * Cisoide de Diocles. Disponible en:[http://es.wikipedia.org/wiki/Cisoide_de_Diocles Wikipedia].Citado 8 de agosto de 2011 |
| − | |||
| − | |||
[[Category:Matemáticas]][[Category:Geometría]] | [[Category:Matemáticas]][[Category:Geometría]] | ||
última versión al 19:56 31 jul 2019
| ||||||
Cisoide de Diocles. cisoide generado por el vector posición de una recta paralela al eje OY (Curva 1), que pasa por el punto (2a,0), al que se le resta el radio vector de una circunferencia de radio a y centro en (0,a)(Curva 2).
Historia
Diocles fue un matemático griego que ideó esta curva con el objetivo de resolver el problema de la duplicación del cubo.
Construyó la curva limitándose a los puntos interiores al círculo. Completando este arco de la curva con la semicircunferencia, se obtiene una forma parecida a una hoja de hiedra, de donde le viene el nombre de cisoide.
Definición
La cisoide se define como el lugar geométrico de los puntos C que verifican que |OA| = |BC|.
Ecuaciones
- Su ecuación cartesiana es:
- La ecuaciones paramétricas es:
x = a sen2 q
y = a sen3 q /cos q
- En coordenadas polares es:
Vea también
Fuentes
- Cisoide de Diocles. Disponible en:Personales ya. Citado 8 de agosto de 2011
- Cisoide de Diocles. Disponible en:Wikipedia.Citado 8 de agosto de 2011