Diferencia entre revisiones de «Lemniscata de Bernoulli»
m (Texto reemplazado: «<div align="justify">» por «») |
|||
| (No se muestran 2 ediciones intermedias de otro usuario) | |||
| Línea 5: | Línea 5: | ||
|concepto= | |concepto= | ||
}} | }} | ||
| − | + | ||
'''Lemniscata de Bernoulli'''. En matemática, una lemniscata es un tipo de curva descrita por la siguiente ecuación en [http://es.wikipedia.org/wiki/Coordenadas_cartesianas coordenadas cartesianas]: | '''Lemniscata de Bernoulli'''. En matemática, una lemniscata es un tipo de curva descrita por la siguiente ecuación en [http://es.wikipedia.org/wiki/Coordenadas_cartesianas coordenadas cartesianas]: | ||
| + | |||
[[Image:Lemniscata.png]] | [[Image:Lemniscata.png]] | ||
| + | |||
== Historia == | == Historia == | ||
| + | |||
La Lemniscata se considera actualmente como un caso particular de los [http://es.wikipedia.org/wiki/%C3%93valo óvalos] estudiados por [[Jean Dominique Cassini]] en [[1680]], pero son [[Jackob Bernoulli]] y [[Johann Bernoulli]] los que la descubrieron y dieron a conocer independientemente, al intentar resolver un problema planteado por [[Leibnitz]] creador, junto con [[Isaac Newton]] del cálculo infinitesimal, que lanzó a la comunidad científica de la época el reto de encontrar la [[ecuación]] de la isócrona paracéntrica. La solución encontrada fue la Lemniscata que en honor a los hermanos Bernoulli paso a denominarse Lemniscata de Bernoulli. | La Lemniscata se considera actualmente como un caso particular de los [http://es.wikipedia.org/wiki/%C3%93valo óvalos] estudiados por [[Jean Dominique Cassini]] en [[1680]], pero son [[Jackob Bernoulli]] y [[Johann Bernoulli]] los que la descubrieron y dieron a conocer independientemente, al intentar resolver un problema planteado por [[Leibnitz]] creador, junto con [[Isaac Newton]] del cálculo infinitesimal, que lanzó a la comunidad científica de la época el reto de encontrar la [[ecuación]] de la isócrona paracéntrica. La solución encontrada fue la Lemniscata que en honor a los hermanos Bernoulli paso a denominarse Lemniscata de Bernoulli. | ||
| Línea 34: | Línea 37: | ||
== Construcción == | == Construcción == | ||
| − | [[Image: | + | [[Image:lemniscata1.png|thumb|right|Lemniscata de Bernoulli]] Se construye una [[Circunferencia|circunferencia]] de centro F’, [[Tangente|tangente]] a dos [[Rectas_Perpendiculares|rectas perpendiculares]] que se cortan en el punto O. |
Sea P un punto cualquiera de la circunferencia y Q el punto de intersección entre la [[Recta|semirrecta OP]] y la circunferencia. Se traza la circunferencia de centro O y radio PQ. | Sea P un punto cualquiera de la circunferencia y Q el punto de intersección entre la [[Recta|semirrecta OP]] y la circunferencia. Se traza la circunferencia de centro O y radio PQ. | ||
última versión al 21:08 12 ago 2019
| ||||
Lemniscata de Bernoulli. En matemática, una lemniscata es un tipo de curva descrita por la siguiente ecuación en coordenadas cartesianas:
Historia
La Lemniscata se considera actualmente como un caso particular de los óvalos estudiados por Jean Dominique Cassini en 1680, pero son Jackob Bernoulli y Johann Bernoulli los que la descubrieron y dieron a conocer independientemente, al intentar resolver un problema planteado por Leibnitz creador, junto con Isaac Newton del cálculo infinitesimal, que lanzó a la comunidad científica de la época el reto de encontrar la ecuación de la isócrona paracéntrica. La solución encontrada fue la Lemniscata que en honor a los hermanos Bernoulli paso a denominarse Lemniscata de Bernoulli.
Bernoulli la llamó lemniscus, que en Latín significa "cinta colgante".
La representación gráfica de esta ecuación genera una curva similar a ∞. La curva se ha convertido en el símbolo del infinito y es ampliamente utilizada en matemática.
Definición
Es la curva que se define como el lugar geométrico de los puntos tales que la suma de las distancias desde dos puntos focales es una constante.
Ecuaciones
- Ecuación en coordenadas cartesianas:
- La lemniscata puede ser descrita mediante coordenadas polares según la siguiente ecuación:
r2=a2cos2θ
- Análogamente, con coordenadas bipolares su ecuación es:
rrʼ=a2/2
Construcción
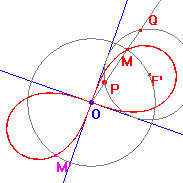
Se construye una circunferencia de centro F’, tangente a dos rectas perpendiculares que se cortan en el punto O.
Sea P un punto cualquiera de la circunferencia y Q el punto de intersección entre la semirrecta OP y la circunferencia. Se traza la circunferencia de centro O y radio PQ.
Sea M el punto de intersección de la semirrecta y la circunferencia de centro O.
El lugar geométrico descrito por el punto M y el simétrico de M respecto a O (M’), a medida que P se mueve en la circunferencia de centro F’, es una Lemniscata de Bernuolli.
Vea también
Fuentes
- Lemniscata [citado 2011 agosto, 18]; Disponible en:http:http://es.wikipedia.org/wiki/Lemniscata.
- Ecuaciones Lemniscata[citado 2011 agosto, 18]; Disponible en:http://www.librosmaravillosos.com/curvasmaravillosas/curvasmaravillosas.html ]