Diferencia entre revisiones de «Monoide»
(Página creada con '{{Definición|nombre=Monoide|imagen=Matemática.jpg|concepto=Estructura algebraica de un conjunto y una operación sobre éste que es cerrada y asociativa, además de que existe...') |
|||
| Línea 1: | Línea 1: | ||
| − | {{Definición|nombre=Monoide|imagen=Matemática.jpg|concepto=Estructura algebraica de un conjunto y una operación sobre éste que es cerrada y asociativa, además de que existe un neutro en el conjunto para la | + | {{Definición|nombre=Monoide|imagen=Matemática.jpg|concepto=Estructura algebraica de un conjunto y una operación sobre éste que es cerrada y asociativa, además de que existe un neutro en el conjunto para la operación.}} |
<div align="justify"> | <div align="justify"> | ||
'''Monoide'''. En [[Álgebra]] dícese de la [[estructura algebraica]] conformada por el par ''<G,*>'', tales que ''G'' es un [[conjunto]] no vacío y ''*'' es una [[operación binaria]]; entonces se cumple que ''*'' es [[Clausura|cerrada]] y [[Asociatividad|asociativa]] y que existe el elemento neutro en ''G'' para ''*''. | '''Monoide'''. En [[Álgebra]] dícese de la [[estructura algebraica]] conformada por el par ''<G,*>'', tales que ''G'' es un [[conjunto]] no vacío y ''*'' es una [[operación binaria]]; entonces se cumple que ''*'' es [[Clausura|cerrada]] y [[Asociatividad|asociativa]] y que existe el elemento neutro en ''G'' para ''*''. | ||
| Línea 16: | Línea 16: | ||
==Ejemplos.== | ==Ejemplos.== | ||
* Los [[Número entero|enteros]] y la suma conforman un monoide pues la suma es cerrada y asociativa, el 0 es el neutro. | * Los [[Número entero|enteros]] y la suma conforman un monoide pues la suma es cerrada y asociativa, el 0 es el neutro. | ||
| − | * Los [[Número natural|números naturales]] y el producto son | + | * Los [[Número natural|números naturales]] y el producto son también un monoide donde el 1 es el neutro de la [[multiplicacion]]. |
| − | * Las [[Cadena de | + | * Las [[Cadena de carácter|cadenas de carácteres]] y la [[concatenación]] forman un monoide teniendo a la [[cadena vacía]] por neutro. |
| − | * Sea un grupo ''<M,*>'' cualquiera, | + | * Sea un grupo ''<M,*>'' cualquiera, también es un monoide. |
==Fuentes.== | ==Fuentes.== | ||
| Línea 25: | Línea 25: | ||
</div> | </div> | ||
| − | [[ | + | [[Categoría:Campos,_anillos,_álgebras]][[Categoría:Álgebra]][[Categoría:Matemáticas]] |
Revisión del 22:35 25 ene 2012
| ||||||
Monoide. En Álgebra dícese de la estructura algebraica conformada por el par <G,*>, tales que G es un conjunto no vacío y * es una operación binaria; entonces se cumple que * es cerrada y asociativa y que existe el elemento neutro en G para *.
En el caso que <G,*> sea monoide y la operación sea conmutativa se dice que es un monoide conmutativo o abeliano.
Definición.
Sea un conjunto G y la operación binaria * definida como *(x,y)=z o mejor x*y=z y se satisfacen cada uno de los siguientes axiomas:
- Clausura:
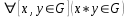 . * es cerrada.
. * es cerrada. - Asociatividad: Para todo x, y, z de G, (x*y)*z=x*(y*z).
- Existencia del neutro: Existe uno y solo un elemento e de G tal que para todo x de G se cumple que x*e=e*x=x. e es llamado neutro para * en G.
Se dice que G con la operación * es un monoide.
Ejemplos.
- Los enteros y la suma conforman un monoide pues la suma es cerrada y asociativa, el 0 es el neutro.
- Los números naturales y el producto son también un monoide donde el 1 es el neutro de la multiplicacion.
- Las cadenas de carácteres y la concatenación forman un monoide teniendo a la cadena vacía por neutro.
- Sea un grupo <M,*> cualquiera, también es un monoide.
Fuentes.
- Carl B. Allendoerfer, Cletus O. Oakley. Introducción moderna a la matemática superior. Ediciones del Castillo, Madrid. 1967.
- Monoide en Wikipedia
