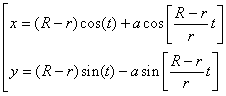Diferencia entre revisiones de «Hipocicloide»
(Página creada con '{{Desarrollo}} {{Definición |nombre=Hipocicloide |imagen=Hipocicloid.jpeg |tamaño= |concepto= Hipocicloide }} <div align="justify"> '''Hipocicloide'''. Es la curva plana gen...') |
|||
| Línea 2: | Línea 2: | ||
{{Definición | {{Definición | ||
|nombre=Hipocicloide | |nombre=Hipocicloide | ||
| − | |imagen= | + | |imagen=Astroide.gif |
|tamaño= | |tamaño= | ||
|concepto= Hipocicloide | |concepto= Hipocicloide | ||
| Línea 22: | Línea 22: | ||
Casos particulares de hipocicloides ordinarias: | Casos particulares de hipocicloides ordinarias: | ||
| − | |||
* Si R = 4r se obtiene la curva llamada astroide. | * Si R = 4r se obtiene la curva llamada astroide. | ||
| Línea 33: | Línea 32: | ||
Las "hipocicloides acortadas" (hipotrocoides cortos) son curvas que se pueden obtener con un Spirograph, haciendo rodar un círculo interior sobre otro círculo, que permanece fijo, colocando un bolígrafo en cualquier punto (agujero) del círculo que rueda. | Las "hipocicloides acortadas" (hipotrocoides cortos) son curvas que se pueden obtener con un Spirograph, haciendo rodar un círculo interior sobre otro círculo, que permanece fijo, colocando un bolígrafo en cualquier punto (agujero) del círculo que rueda. | ||
| − | |||
| − | Casos particulares de hipocicloides | + | Casos particulares de hipocicloides acortadas: |
| + | * Si R=2r y a=0, P está en el centro del círculo móvil y describe una circunferencia. | ||
| − | + | * Si R=2r y a<>0 P no está en el borde del círculo ni en el centro y describe una elipse. | |
| − | * Si | ||
| − | |||
| − | |||
=== Hipocicloides alargadas === | === Hipocicloides alargadas === | ||
| Línea 54: | Línea 50: | ||
== Ecuaciones == | == Ecuaciones == | ||
| − | * [[Ecuación| | + | * Las [[Ecuación|ecuaciones]] paramétricas suelen escribirse como: |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | [[Image:F_hipociclo_1.0.png]] | |
| − | |||
| − | |||
| − | |||
| − | + | [[Image:F_hipociclo_2.png]] | |
| − | < | + | La ecuación en coordenadas cartesianas del hipocicloide (astroide) de cuatro puntas (cuando r<sub>1</sub>=4r<sub>2</sub>) es: |
| − | + | [[Image:Ecuac_hipocic.png ]] | |
== Propiedades == | == Propiedades == | ||
Revisión del 11:52 22 ago 2011
| ||||||
Hipocicloide. Es la curva plana generada por el movimiento de un punto de una circunferencia que rueda, sin deslizamiento, por el interior de otra circunferencia.
Sumario
Definición
LA Hipocicloide es la curva que describe la trayectoria un punto situado sobre una circunferencia generatriz que rueda por el interior de otra circunferencia directriz, sin deslizamiento. Es un tipo de ruleta cicloidal.
Dentro de esta familia de curvas se encuentran:
Hipocicloides ordinarias
Las hipocicloides ordinarias (hipocicloides) son curvas generadas por un punto P de una circunferencia de radio r al girar interiormente y sin deslizamiento sobre otra circunferencia de radio R. (r<R)
La curva generada depende de la relación entre los radios de ambas circunferencias. Hay que señalar que si n=R/res entero, la hipocicloide generada por el punto P se cerrará al cabo de una vuelta, y podremos observar que tiene n cúspides.
Casos particulares de hipocicloides ordinarias:
- Si R = 4r se obtiene la curva llamada astroide.
- Si R = 3r se obtiene la hipocicloide de Steiner (de Cremona) o deltoide (que se asemeja a un delta)
- Si R=2r se obtiene un segmento (diámetro del círculo de radio r) llamada "Mosca del Hire".
Hipocicloides acortadas
Las "hipocicloides acortadas" (hipotrocoides cortos) son curvas que se pueden obtener con un Spirograph, haciendo rodar un círculo interior sobre otro círculo, que permanece fijo, colocando un bolígrafo en cualquier punto (agujero) del círculo que rueda.
Casos particulares de hipocicloides acortadas:
- Si R=2r y a=0, P está en el centro del círculo móvil y describe una circunferencia.
- Si R=2r y a<>0 P no está en el borde del círculo ni en el centro y describe una elipse.
Hipocicloides alargadas
Las "hipocicloides alargadas" (hipotrocoides largos) son curvas generadas de modo análogo a las hipotrocoides cortas pero en las que el punto P es un punto vinculado al círculo que rueda pero dentro del disco La ecuación general de las epicicloides alargadas se obtiene de análoga forma que la de la acortada, solamente tenemos que tener presente que a>r
Historia
Ecuaciones
- Las ecuaciones paramétricas suelen escribirse como:
La ecuación en coordenadas cartesianas del hipocicloide (astroide) de cuatro puntas (cuando r1=4r2) es:
Propiedades
Aplicaciones
Vea también
Fuentes
- Cicloide [citado 2011 agosto, 18]; Disponible en:[1].
- La cicloide [citado 2011 agosto, 18]; Disponible en:[2]