Diferencia entre revisiones de «Semigrupo conmutativo»
(Página creada con '{{Definición|nombre=Semigrupo conmutativo|imagen=Matemática.jpg|concepto=Estructura algebraica de un conjunto y una operación sobre éste que es cerrada, asociativa y conmuti...') |
(→Ejemplos.) |
||
| Línea 15: | Línea 15: | ||
==Ejemplos.== | ==Ejemplos.== | ||
| − | + | * Todo [[grupo conmutativo]] ''<G,*>'' es un semigrupo conmutativo. | |
| − | + | * Los siguientes son semigrupos abelianos representados en forma tabular: | |
| − | |||
{| class="wikitable" | {| class="wikitable" | ||
!''<{a,b},@>'' | !''<{a,b},@>'' | ||
| Línea 46: | Línea 45: | ||
|} | |} | ||
|} | |} | ||
| − | + | * Es un semigrupo conmutativo las matrices complejas [[Archivo:M_sub_n_m_de_C.gif|middle]] con la operación suma de matrices definidas de la manera tradicional: | |
| − | + | ** [[Archivo:Suma_matrices.gif|middle]] con [[Archivo:A_B_en_M_sub_m_n_C.gif|middle]] y [[Archivo:A_B_en_C.gif|middle]] | |
| − | |||
==Fuentes.== | ==Fuentes.== | ||
Revisión del 13:53 27 ene 2012
| ||||||
Semigrupo conmutativo o abeliano. En Álgebra dícese de la estructura algebraica conformada por el par <G,*>, tales que G es un conjunto no vacío y * es una operación binaria; entonces se cumple que * es cerrada, asociativa y conmutativa.
Definición.
Sea un conjunto G y la operación binaria * definida como *(x,y)=z, normalmente escrita como x*y=z que satisface los axiomas:
- Clausura:
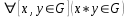 . * es cerrada.
. * es cerrada. - Asociatividad: Para todo x, y, z de G, (x*y)*z=x*(y*z).
- Conmutatividad: Para todo x, y de G, x*y=y*x.
Se dice que G con la operación * es un semigrupo conmutativo o abeliano.
En otras palabras, un semigrupo abeliano es un grupo cuya operación también es conmutativa.
Ejemplos.
- Todo grupo conmutativo <G,*> es un semigrupo conmutativo.
- Los siguientes son semigrupos abelianos representados en forma tabular:
| <{a,b},@> | <{a,b,c},*> | |||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
- Es un semigrupo conmutativo las matrices complejas
 con la operación suma de matrices definidas de la manera tradicional:
con la operación suma de matrices definidas de la manera tradicional:
Fuentes.
- Carl B. Allendoerfer, Cletus O. Oakley. Introducción moderna a la matemática superior. Ediciones del Castillo, Madrid. 1967.

