Diferencia entre revisiones de «Subgrupo conmutativo»
(Página creada con '{{Definición|nombre=Subgrupo conmutativo|imagen=Matemática.jpg|concepto=Sea el subgrupo ''<G',*>'' cuya operación ''*'' es conmutativa; se dice que ''<G',*>'' es un subgr...') |
|||
| Línea 64: | Línea 64: | ||
==Fuentes.== | ==Fuentes.== | ||
| − | # Carl B. Allendoerfer, Cletus O. Oakley. Introducción moderna a la matemática superior. Ediciones del Castillo, Madrid. 1967. | + | # Carl B. Allendoerfer, Cletus O. Oakley. Introducción moderna a la matemática superior. Ediciones del Castillo, [[Madrid]]. [[1967]]. |
| − | # [http://es.wikipedia.org/wiki/ | + | # [http://es.wikipedia.org/wiki/Subgrupo Subgrupo en Wikipedia]. Consultado [[22 de febrero]] de [[2012]]. |
</div> | </div> | ||
[[Categoría:Campos,_anillos,_álgebras]][[Categoría:Matemáticas]][[Categoría:Álgebra]] | [[Categoría:Campos,_anillos,_álgebras]][[Categoría:Matemáticas]][[Categoría:Álgebra]] | ||
Revisión del 19:02 22 feb 2012
| ||||||
Subgrupo conmutativo. En Álgebra dícese de la estructura algebraica conformada por el par <G',*> que conforma un subgrupo y * es una operación binaria yconmutativa. También es equivalente a decir subgrupo abeliano.
Sumario
Definición.
- Sea un conjunto G y la operación binaria * tales que <G,*> conforman un grupo algebraico, se le llama subgrupo conmutativo o abeliano a cualquier
 con
con 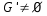 que satisfaga el hecho de ser también un grupo sobre la misma operación * y que además para todos x e y de G' se cumple que x*y=y*x.
que satisfaga el hecho de ser también un grupo sobre la misma operación * y que además para todos x e y de G' se cumple que x*y=y*x.
Una consecuencia de importancia en los subgrupos conmutativos es la siguiente:
- El subgrupo trivial <{e},*> es siempre conmutativo.
Ejemplos.
Ejemplo 1.
El menor de los subgrupos conmutativos del grupo <G,*> es <{e},*> donde e es el elemento neutro para * en G, es decir el subgrupo trivial.
=Ejemplo 2.
Sea el grupo <{0;1;2;3;4},+5> cuya operación +5 (suma módulo 5) viene definida por la tabla:
| +5 | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| 0 | 0 | 1 | 2 | 3 | 4 |
| 1 | 1 | 2 | 3 | 4 | 0 |
| 2 | 2 | 3 | 4 | 0 | 1 |
| 3 | 3 | 4 | 0 | 1 | 2 |
| 4 | 4 | 0 | 1 | 2 | 3 |
no tiene otro subgrupo que el trivial, porque para el resto de los subconjuntos de G se incumple el axioma del cierre de los grupos.
Ejemplo 3.
Sea el grupo <{e,a,b,c},@> (Grupo Cuarto de Klein) con @ definida según la tabla siguiente:
| @ | e | a | b | c |
|---|---|---|---|---|
| e | e | a | b | c |
| a | a | e | c | b |
| b | b | c | e | a |
| c | c | b | a | e |
tiene a <{e},@>, <{e,a},@> por subgrupos conmutativos.
Ejemplo 4.
Sea el subconjunto real [0;1] y el producto aritmético estos constituyen un subgrupo conmutativo de los números reales, no así el mismo subconjunto y la suma, porque no es cerrada e incumple la existencia del inverso por ejemplo para 1.
Fuentes.
- Carl B. Allendoerfer, Cletus O. Oakley. Introducción moderna a la matemática superior. Ediciones del Castillo, Madrid. 1967.
- Subgrupo en Wikipedia. Consultado 22 de febrero de 2012.
